Question

过△ABC所在平面α外一点P，作PO⊥α，若O点为△ABC的外心，则（　　）

A．PA=PB=PC

B．AO⊥BC

C．PA⊥平面PBC

D．AB=BC=AC

Answer 1

分析：点P为△ABC所在平面外一点，PO⊥α，垂足为O，若O点为△ABC的外心，则OA=OB=OC，可证得△POA≌△POB≌△POC，从而证得PA=PB=PC．

解答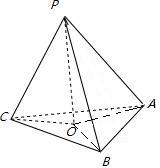：证明：点P为△ABC所在平面外一点，PO⊥α，垂足为O，
若O点为△ABC的外心，
则OA=OB=OC
又∵△POA，△POB，△POC都是直角三角形
∵PO是公共边，OA=OB=OC
∴△POA≌△POB≌△POC
∴PA=PB=PC
故选A

点评：本题考查三角形五心，求解本题的关键是能够根据题设条件得出PA，PB，PC相等，以及熟练掌握三角形个心的定义，本题是一个判断形题，是对基本概念的考查题．