题目内容

在可导函数f（x）中，已知f（1）=2，f′（1）=-1，则
lim
x→1
2x-f(x)
x-1
=（　　）
A、1B、3C、5D、8
分析：由题设知
lim
x→1
2x-f(x)
x-1
=
lim
x→1
2x-[f(x)-2]-2
x-1
=-
lim
x→1
f(x-2)
x-1
+
lim
x→1
2(x-1)
x-1
=-f′（1）+2，由此能求出结果．
解答：解：∵f′（1）=
lim
x→1
f(x)-f(1)
x-1
=
lim
x→1
f(x)-2
x-1
=-1
∴
lim
x→1
2x-f(x)
x-1

=
lim
x→1
2x-[f(x)-2]-2
x-1

=-
lim
x→1
f(x-2)
x-1
+
lim
x→1
2(x-1)
x-1

=-f′（1）+2=3
故选B．
点评：本题考查极限的概念和应用，解题时要熟练掌握极限的概念，正确理解极限和导数间的相互关系．
练习册系列答案
相关题目
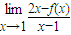有一段“三段论”推理是这样的：对于可导函数f（x），如果f′（x0）=0，那么x=x0是函数f（x）的极值点，因为函数f（x）=x3在x=0处的导数值f′（0）=0，所以，x=0是函数f（x）=x3的极值点．以上推理中（　　）
定义在（m，n）上的可导函数f（x）的导数为f'（x），若当x∈[a，b]?（m，n）时，有|f'（x）|≤1，则称函数f（x）为[a，b]上的平缓函数．下面给出四个结论：
①y=cosx是任何闭区间上的平缓函数；
②y=x2+lnx是[
1
2
，1]上的平缓函数；
③若f（x）=
1
3
x3-mx2-3m2x+1是[0，
1
2
]上的平缓函数，则实数m的取值范围是[-
3
3
，
1
2
]；
④若y=f（x）是[a，b]上的平缓函数，则有|f（a）-f（b）|≤|a-b|．
这些结论中正确的是
①③④
①③④
（多填、少填、错填均得零分）．
设集合M是满足下列条件的函数f（x）的集合：①f（x）的定义域为R；②存在a＜b，使f（x）在（-∞，a），（b，+∞）上分别单调递增，在（a，b）上单调递减．
（I）设f1（x）=x•|x-2|，f2（x）=x3-3x2+3x，判断f1（x），f2（x）是否在集合M中，并说明理由；
（II）求证：对任意的实数t，f（x）=
-x+tx2+1
都在集合M中；
（Ⅲ）是否存在可导函数f（x），使得f（x）与g（x）=f'（x）-x都在集合M中，并且有相同的单调区间？请说明理由．
在可导函数f（x）中，已知f（1）=2，f′（1）=-1，则=（ ）
A．1
B．3
C．5
D．8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网