题目内容
(本题满分14分)已知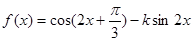 ,且
,且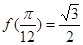 .
.
(1)求实数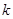 的值;
的值;
(2)求函数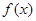 的单调递增区间及最大值,并指出取得最大值时的
的单调递增区间及最大值,并指出取得最大值时的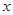 值.
值.
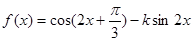 ,且
,且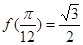 .
.(1)求实数
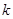 的值;
的值;(2)求函数
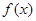 的单调递增区间及最大值,并指出取得最大值时的
的单调递增区间及最大值,并指出取得最大值时的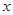 值.
值. (1) ;(2)
;(2)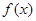 的单调递增区间为
的单调递增区间为 (
( ),
), 时,函数
时,函数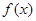 的最大值为
的最大值为 。
。
 ;(2)
;(2)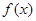 的单调递增区间为
的单调递增区间为 (
( ),
), 时,函数
时,函数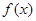 的最大值为
的最大值为 。
。本试题主要是考查了三角函数的 性质和变换的综合运用。
(1)先根据已知表达式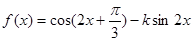 ,和
,和 ,得到k的值,然后化为单一函数得到结论
,得到k的值,然后化为单一函数得到结论 。
。
(2)在 的情况下,对于单调性和最值分别分析得到结论。
的情况下,对于单调性和最值分别分析得到结论。
解:(1)由已知 ,得
,得 ,-----------4分
,-----------4分
(2)
 --------8分
--------8分
由 得
得 ,
,

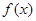 的单调递增区间为
的单调递增区间为 (
( )-----------------11分
)-----------------11分
又当 (
( ),
),
即 时,函数
时,函数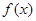 的最大值为
的最大值为 。---------------14分
。---------------14分
(1)先根据已知表达式
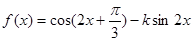 ,和
,和 ,得到k的值,然后化为单一函数得到结论
,得到k的值,然后化为单一函数得到结论 。
。(2)在
 的情况下,对于单调性和最值分别分析得到结论。
的情况下,对于单调性和最值分别分析得到结论。解:(1)由已知
 ,得
,得 ,-----------4分
,-----------4分(2)

 --------8分
--------8分由
 得
得 ,
,
 的单调递增区间为
的单调递增区间为 (
( )-----------------11分
)-----------------11分又当
 (
( ),
),即
 时,函数
时,函数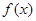 的最大值为
的最大值为 。---------------14分
。---------------14分
练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目


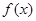 的定义域是
的定义域是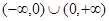 ,且
,且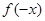 =
=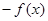 .已知当x>0时
.已知当x>0时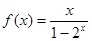
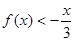 .
. 上的两个函数:
上的两个函数: ,
,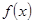 在
在 ,若对任意的
,若对任意的

 =
= 成
成 的取值范围是 .
的取值范围是 .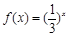 , 其反函数为
, 其反函数为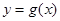
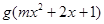 的定义域为
的定义域为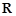 ,求实数
,求实数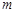 的取值范围;
的取值范围;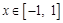 时,求函数
时,求函数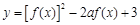 的最小值
的最小值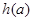 ;
;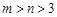 ,使得函数
,使得函数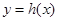 的定义域为
的定义域为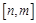 ,值域为
,值域为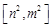 ,若存在,求出
,若存在,求出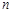 的值;若不存在,则说明理由.
的值;若不存在,则说明理由. ax 3 + x2 + 2 ( a ≠ 0 ) .
ax 3 + x2 + 2 ( a ≠ 0 ) . 是连续的偶函数,且当x>o时,
是连续的偶函数,且当x>o时, 的所有x为之和______________________________
的所有x为之和______________________________ ,则
,则 ( )
( )
