题目内容
如图,P﹣ABCD是正四棱锥,ABCD﹣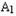
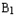
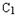
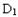 是正方体,其中
是正方体,其中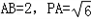 .
.
(1)求证PA⊥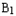
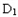 ;
;
(2)求平面PAD与平面BD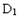
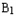 所成的锐二面角θ的正弦值大小;
所成的锐二面角θ的正弦值大小;
(3)求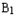 到平面PAD的距离.
到平面PAD的距离.
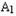
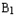
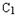
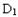 是正方体,其中
是正方体,其中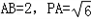 .
.(1)求证PA⊥
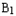
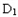 ;
;(2)求平面PAD与平面BD
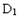
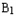 所成的锐二面角θ的正弦值大小;
所成的锐二面角θ的正弦值大小;(3)求
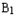 到平面PAD的距离.
到平面PAD的距离.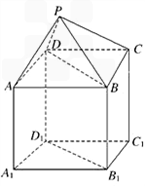
(1)证明以
 为x轴,
为x轴,
 为y轴,
为y轴, A为z轴,建立空间直角坐标系,
A为z轴,建立空间直角坐标系,
设E为BD的中点,
∵P﹣ABCD是正四棱锥,
∴PE⊥平面ABCD,
∵ ,
,
∴PE=2,
∴P(1,1,4),
∴ ,
, ,
,
∴ ,
,
故PA⊥
 .
.
(2)解:设平面PAD的法向量 ,
,
∵ ,
, ,
,
∴ ,
,
∴ .
.
∵平面BD
 的法向量
的法向量 ,
,
∴cos< >=
>= =﹣
=﹣ ,
,
∴ =
= .
.
(3)解:∵ ,
,
∴ 到平面PAD的距离d=
到平面PAD的距离d= =
= .
.

 为x轴,
为x轴,
 为y轴,
为y轴, A为z轴,建立空间直角坐标系,
A为z轴,建立空间直角坐标系,设E为BD的中点,
∵P﹣ABCD是正四棱锥,
∴PE⊥平面ABCD,
∵
 ,
,∴PE=2,
∴P(1,1,4),
∴
 ,
, ,
,∴
 ,
,故PA⊥

 .
.(2)解:设平面PAD的法向量
 ,
,∵
 ,
, ,
,∴
 ,
,∴
 .
.∵平面BD

 的法向量
的法向量 ,
,∴cos<
 >=
>= =﹣
=﹣ ,
,∴
 =
= .
.(3)解:∵
 ,
,∴
 到平面PAD的距离d=
到平面PAD的距离d= =
= .
.
练习册系列答案
相关题目
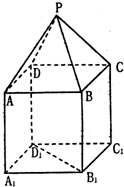 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
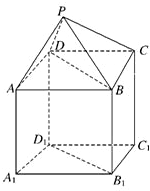 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA= 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=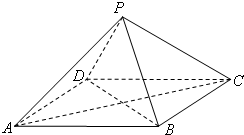 如图,P-ABCD是正四棱锥,
如图,P-ABCD是正四棱锥, 如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知
如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知