题目内容
函数 的定义域为R,并满足以下条件:①对任意
的定义域为R,并满足以下条件:①对任意 ,有
,有 ;
;
②对任意 、
、 ,有
,有 ;③
;③ 则
则
(1)求 的值; (4分)
的值; (4分)
(2)求证: 在R上是单调增函数; (5分)
在R上是单调增函数; (5分)
(3)若 ,求证:
,求证:
 的定义域为R,并满足以下条件:①对任意
的定义域为R,并满足以下条件:①对任意 ,有
,有 ;
;②对任意
 、
、 ,有
,有 ;③
;③ 则
则(1)求
 的值; (4分)
的值; (4分) (2)求证:
 在R上是单调增函数; (5分)
在R上是单调增函数; (5分)(3)若
 ,求证:
,求证:
(1)
(2)证明见解析
(3)证明见解析

(2)证明见解析
(3)证明见解析
解法一:(1)令 ,得:
,得: ……………1分
……………1分
 …………………………4分
…………………………4分
(2)任取 、
、 ,且
,且 . 设
. 设 则
则
 …………………… 8分
…………………… 8分
 在R上是单调增函数…… 9分
在R上是单调增函数…… 9分
(3)由(1)(2)知


 ………11分
………11分 
而
 ……15分
……15分
解法二:(1)∵对任意x、y∈R,有
 ………1分 ∴当
………1分 ∴当 时
时 ……2分
……2分
∵任意x∈R, …………3分
…………3分  ……………………4分
……………………4分
(2) …………………………6分
…………………………6分
 是R上单调增函数 即
是R上单调增函数 即 是R上单调增函数;…… 9分
是R上单调增函数;…… 9分
(3) ……………………11分
……………………11分
而

 ,得:
,得: ……………1分
……………1分 …………………………4分
…………………………4分(2)任取
 、
、 ,且
,且 . 设
. 设 则
则
 …………………… 8分
…………………… 8分 在R上是单调增函数…… 9分
在R上是单调增函数…… 9分(3)由(1)(2)知



 ………11分
………11分 
而

 ……15分
……15分解法二:(1)∵对任意x、y∈R,有

 ………1分 ∴当
………1分 ∴当 时
时 ……2分
……2分∵任意x∈R,
 …………3分
…………3分  ……………………4分
……………………4分(2)
 …………………………6分
…………………………6分 是R上单调增函数 即
是R上单调增函数 即 是R上单调增函数;…… 9分
是R上单调增函数;…… 9分(3)
 ……………………11分
……………………11分而



练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
 与销售数量
与销售数量 的函数关系式;
的函数关系式; –(2a)2]对任意x∈[
–(2a)2]对任意x∈[ ,+∞]都有意义,则实数a的取值范围是( )
,+∞]都有意义,则实数a的取值范围是( )


 )
) .
. .
.
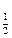 (a2-ax+2a)在[1,+∞
(a2-ax+2a)在[1,+∞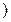 上为减函数,则实数a的取值范围是( )
上为减函数,则实数a的取值范围是( )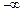 ,0)
,0)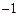 ,0)
,0)
 ,则
,则 的值为__________。
的值为__________。 ,则
,则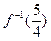 =
=