题目内容
已知命题p:方程![]() =1表示焦点在y轴上的椭圆;命题q:方程x2=(4m2﹣m)y表示焦点在y轴正半轴上的抛物线.若“p∧q”为真命题,则实数m的取值范围是 .
=1表示焦点在y轴上的椭圆;命题q:方程x2=(4m2﹣m)y表示焦点在y轴正半轴上的抛物线.若“p∧q”为真命题,则实数m的取值范围是 .
考点:
复合命题的真假.
专题:
圆锥曲线的定义、性质与方程.
分析:
由p∧q为真命题,知命题p和命题q都是真命题,由此利用抛物线和椭圆性质能求出实数m的取值范围.
解答:
解:∵p∧q为真命题,
∴命题p:方程![]() =1表示焦点在y轴上的椭圆是真命题,
=1表示焦点在y轴上的椭圆是真命题,
q:方程x2=(4m2﹣m)y表示焦点在y轴正半轴上的抛物线是真命题.
当命题p是真命题时,0<m<1;
当命题q为真命题时,4m2﹣m>0,解得m<0,或m>![]() .
.
∴当p∧q为真命题时,实数m的取值范围是(![]() ,1).
,1).
故答案为:(![]() ,1).
,1).
点评:
本题考查直线与圆锥曲线的位置关系的应用,解题时要认真审题,注意复合命题真假判断的灵活运用.

练习册系列答案
相关题目
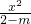 +
+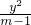 =1的图象是焦点在y轴上的双曲线;命题q:方程4x2+4(m-2)x+1=0无实根;又 p∨q为真,¬q为真,求实数m的取值范围.
=1的图象是焦点在y轴上的双曲线;命题q:方程4x2+4(m-2)x+1=0无实根;又 p∨q为真,¬q为真,求实数m的取值范围. +
+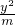 =1表示焦点在y轴上的椭圆,命题q:实数m满足方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线.若“p∧q”为假命题,“p?q”为真命题,求实数m的取值范围.
=1表示焦点在y轴上的椭圆,命题q:实数m满足方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线.若“p∧q”为假命题,“p?q”为真命题,求实数m的取值范围. =1表示焦点在y轴上的椭圆;命题q:方程x2=(4m2-m)y表示焦点在y轴正半轴上的抛物线.若“p∧q”为真命题,则实数m的取值范围是 .
=1表示焦点在y轴上的椭圆;命题q:方程x2=(4m2-m)y表示焦点在y轴正半轴上的抛物线.若“p∧q”为真命题,则实数m的取值范围是 . +
+ =1表示焦点在y轴上的椭圆,命题q:实数m满足方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线.若“p∧q”为假命题,“p?q”为真命题,求实数m的取值范围.
=1表示焦点在y轴上的椭圆,命题q:实数m满足方程(m+4)x2-(m+2)y2=(m+4)(m+2)为双曲线.若“p∧q”为假命题,“p?q”为真命题,求实数m的取值范围.