题目内容
在等腰Rt△ABC中，在斜边AB上任取一点M，求AM的长小于AC的长的概率.
思路分析：点M随机地落在线段AB上，故线段AB为区域D.当点M位于图中线段AC′上时，AM＜AC.故线段AC′即为区域d.
解：在AB上截取AC′=AC.于是P（AM＜AC)=P(AM＜AC′)=
.
（2）如下图，在等腰Rt△ABC中，过直角顶点C在∠ACB内部任作一条射线CM，与线段AB交于点M，求AM＜AC的概率.
解析：在∠ACB内的射线CM是均匀分布的，所以射线CM作在任何位置都是等可能的.在AB上取AC′=AC，则∠ACC′=67.5°，故满足条件的概率为
=0.75.
练习册系列答案
相关题目
在等腰Rt△ABC中，在斜边AB上任取一点M，求AM的长小于AC的长的概率．在等腰Rt△ABC中，∠A=90°，
=（1，2），
=（m，n）（n＞0）则
=（ ）
| AB |
| AC |
| BC |
| A、（-3，-1） |
| B、（-3，1） |
| C、（3，-1） |
| D、（3，1） |
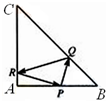在等腰Rt△ABC中，AB=AC=4，点P是边AB上异于A，B的一点，光线从点P出发，经BC，CA反射后又回到原来的点P．若AP=| 4 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|