题目内容
如图,直线l交双曲线
证明:当直线l的斜率不存在时,依据对称性知|AB|=|CD|,
当直线l的斜率存在时,设直线l的方程为y=kx+m.
由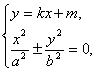
得(b2-a2k2)x2-2a2kmx-a2m2-a2b2=0.
∴AD中点M的横坐标为![]() .
.
由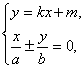 得BC中点N的横坐标为
得BC中点N的横坐标为![]() .∴xm=xn.
.∴xm=xn.
而M、N均在直线l上,∴M、N重合.
∴|AB|=|CD|.
综上|AB|=|CD|.

练习册系列答案
相关题目
题目内容
如图,直线l交双曲线
证明:当直线l的斜率不存在时,依据对称性知|AB|=|CD|,
当直线l的斜率存在时,设直线l的方程为y=kx+m.
由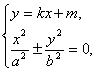
得(b2-a2k2)x2-2a2kmx-a2m2-a2b2=0.
∴AD中点M的横坐标为![]() .
.
由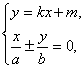 得BC中点N的横坐标为
得BC中点N的横坐标为![]() .∴xm=xn.
.∴xm=xn.
而M、N均在直线l上,∴M、N重合.
∴|AB|=|CD|.
综上|AB|=|CD|.
