题目内容
设函数f(x)=-4x+b,且不等式|f(x)|＜c的解集为{x|-1＜x＜2}.(1)求b的值;
(2)解关于x的不等式(4x+m)f(x)＞0(m∈R).
分析：(1)可先求出|f(x)|＜c的解集,然后与{x|-1＜x＜2}比较.
(2)变形为(x+
)(x-
)＜0.∵-
与
的大小关系不确定,故需分类讨论.
解：(1)|f(x)|＜c
-c＜-4x+b＜c
＜x＜
,
∴
∴
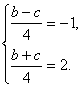(2)f(x)=-4x+2.
由(4x+m)f(x)＞0得(4x+m)(-4x+2)＞0,
∴(x+
)(x-
)＜0.
当m＜-2时,-
＞
,∴
＜x＜-
;
当m=-2时,-
=
,∴原不等式无解;
当m＞-2时,-
＜
,∴-
＜x＜
.
∴当m＜-2时,原不等式的解集为{x|
＜x＜-
};
当m=-2时,原不等式的解集为
;
当m＞-2时,原不等式的解集为{x|-
＜x＜
}.
练习册系列答案
快乐5加2金卷系列答案
相关题目
设函数f(x)=2sin(x-
)cos(x+
)+1，则f（x）是（ ）
| π |
| 4 |
| π |
| 4 |
| A、最小正周期为π的奇函数 |
| B、最小正周期为π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为2π的偶函数 |