题目内容
(2013•盐城二模)函数f(x)=2sin(x-
),x∈[-π,0]的单调递增区间为
| π |
| 4 |
[-
,0]
| π |
| 4 |
[-
,0]
.| π |
| 4 |
分析:由x∈[-π,0]⇒z=x-
∈[-
,-
],利用正弦函数y=sinz在[-
,-
]上单调递增,即可求得答案.
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
解答:解:∵x∈[-π,0]
∴x-
∈[-
,-
],
令z=x-
,则z∈[-
,-
],
∵正弦函数y=sinz在[-
,-
]上单调递增,
∴由-
≤x-
≤-
得:
-
≤x≤0.
∴函数f(x)=2sin(x-
)在x∈[-π,0]的单调递增区间为[-
,0].
故答案为[-
,0].
∴x-
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
令z=x-
| π |
| 4 |
| 5π |
| 4 |
| π |
| 4 |
∵正弦函数y=sinz在[-
| π |
| 2 |
| π |
| 4 |
∴由-
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
-
| π |
| 4 |
∴函数f(x)=2sin(x-
| π |
| 4 |
| π |
| 4 |
故答案为[-
| π |
| 4 |
点评:本题考查正弦函数的单调性,考查整体代入思想的应用,属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
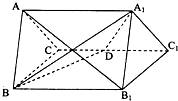 (2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.
(2013•盐城二模)正三棱柱ABC-A1B1C1的所有棱长都为4,D为的CC1中点.