题目内容
设平面内有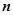
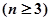条直线，其中有且仅有两条直线互相平行，任意三条直线不过同一点．若用
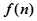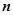表示这条直线交点的个数，则
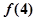= ▲ ；当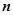＞４时，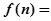
▲ ．
|
|
|
|
|
|
4 |
|
|
|
|
|
【答案】
； 
【解析】解：如图，4条直线有5个交点，
故f（4）=5，
由f（3）=2，
f（4）=f（3）+3
…
f（n-1）=f（n-2）+n-2
f（n）=f（n-1）+n-1
累加可得f（n）=2+3+…+（n-2）+（n-1）=
练习册系列答案
通城学典默写能手系列答案
相关题目
已知椭圆
，抛物线
的焦点均在
轴上，的中心和的顶点均为原点
，每条曲线上取两个点，将其坐标记录于表中：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求，的标准方程；
（2）设斜率不为0的动直线
与有且只有一个公共点
，且与的准线交于
，试探究：在坐标平面内是否存在定点
，使得以
为直径的圆恒过点？若存在，求出点的坐标，若不存在，请说明理由.