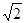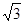题目内容
(本小题满分12分)
△ 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 =3,
=3, =
= ,
, ,
,
(1)求 得值;
得值;
(2)求△ 的面积.
的面积.
△
 中,角
中,角 所对的边分别为
所对的边分别为 ,已知
,已知 =3,
=3, =
= ,
, ,
,(1)求
 得值;
得值;(2)求△
 的面积.
的面积.(1) .(2)
.(2) 的面积
的面积 .
.
 .(2)
.(2) 的面积
的面积 .
.试题分析:(1)应用三角函数同角公式得,
 ,
,再据
 ,求得
,求得 ,进一步应用正弦定理可得解.
,进一步应用正弦定理可得解.(2)由已知,只需进一步确定
 ,结合
,结合 及
及 .
.可得

 .
.应用
 的面积公式即得解.
的面积公式即得解.试题解析:(1)在
 中,
中,由题意知
 ,
,又因为
 ,
,所有
 ,
,由正弦定理可得
 .
.(2)由
 得
得 ,
,由
 ,得
,得 .
.所以



 .
.因此,
 的面积
的面积 .
.
练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
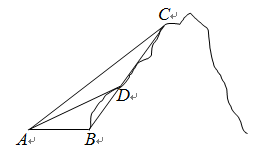
 。
。 的内角
的内角 所对的边分别为
所对的边分别为 .
. ;
; 的最小值.
的最小值. 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知 ,
, ,求B.
,求B.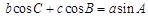 , 则△ABC的形状为( )
, 则△ABC的形状为( ) ,则
,则 =( )
=( )


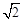 ,则
,则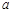 =_____________.
=_____________.