Question

已知抛物线S的顶点在坐标原点,焦点在x轴上,△ABC的三个顶点都在抛物线上,且△ABC的重心为抛物线的焦点,若BC所在直线l的方程为4x+y-20=0.

(1)求抛物线S的方程;

(2)若O是坐标原点,P、Q是抛物线S上的两个动点,且满足OP⊥OQ.试说明动直线PQ是否过定点.

Answer 1

解:(1)设抛物线S的方程为y²=2px..

由可得2y²+py-20p=0..

由Δ＞0,有p＞0,或p＜-160.设B(x₁,y₁),C(x₂,y₂),则y₁+y₂=,

∴x₁+x₂=(5)+(5)=10=10+..

设A(x₃,y₃),由△ABC的重心为F(,0),则=,=0,

∴x₃=-10,y₃=.∵点A在抛物线S上,∴()²=2p(-10).∴p=8..

∴抛物线S的方程为y²=16x..

(2)当动直线PQ的斜率存在时,设PQ的方程为y=kx+b,显然k≠0,b≠0,.

设P(x_P,y_P),Q(x_Q,y_Q),∵OP⊥OQ,∴k_OP·k_OQ=-1.∴·=-1.

∴x_Px_Q+y Py_Q=0.

将y=kx+b代入抛物线方程,得ky²-16y+16b=0,

∴y_Py_Q=.从而x_Px_Q==,∴+=0.

∵k≠0,b≠0,∴b=-16k.

∴动直线方程为y=kx-16k=k(x-16).此时动直线PQ过定点(16,0).

当直线PQ的斜率不存在时,显然PQ⊥x轴,又OP⊥OQ,∴△POQ为等腰直角三角形.

由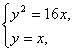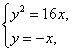得到P(16,16),Q(16,-16).

此时直线PQ亦过点(16,0).

综上所述,动直线PQ过定点M(16,0).