题目内容
已知直三棱柱ABC-A1B1C1中,ΔABC为等腰直角三角形,∠BAC=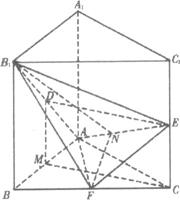
(Ⅰ)求证:DE∥平面ABC;
(Ⅱ)求证:B1F⊥平面AEF;
(Ⅲ)求二面角B1-AE-F的大小.
解法一:(Ⅰ)证明:取AB的中点M,

∵D为B1A中点,∴DM![]()
![]() BB1.
BB1.
又由E是CC1的中点,易得EC![]()
![]() BB1,
BB1,
∴DM![]() EC.
EC.
∴四边形DMCE是平行四边形,
∴DE∥MC.
又DE![]() 平面ABC,MC
平面ABC,MC![]() 平面ABC,
平面ABC,
∴DE∥平面ABC.
(Ⅱ)证明:由已知,△ABC为等腰直角三角形,
∠BAC=90°,F为BC的中点,
∴AF⊥BC.有AF⊥平面BB1C1C.
又B1F![]() 平面BB1C1C,∴B1F⊥AF.
平面BB1C1C,∴B1F⊥AF.
在Rt△B1BF和Rt△FCE中,由已知可得BC=![]() BB1,CC1=BB1,
BB1,CC1=BB1,
∴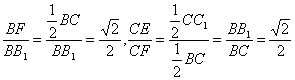 .
.
∴Rt△B1BF∽Rt△FCE,
∴∠BB1F=∠EFC,而∠BB1F+∠B1FB=90°,
∴∠B1FB+∠EFC=90°,
∴∠B1FE=90°,即B1F⊥EF.
又AF∩EF=F,∴B1F⊥平面AEF.
(Ⅲ)解:过F作FN⊥AE于点N,连结B1N,设AB=a,
∵B1F⊥平面AEF,∴B1N⊥AE.
∴∠B1NF为二面角B1-AE-F的平面角.
∵AF⊥平面BB1C1C,EF![]() 平面BB1C1C,
平面BB1C1C,
∴EF⊥AF.
在Rt△AEF中,可求得FN=![]() .
.
在Rt△B1FN中,∠B1FN=90°,
∴tan∠B1NF=![]() .
.
∴∠B1NF=arctan![]() ,即二面角B1-AE-F的大小为arctan
,即二面角B1-AE-F的大小为arctan![]() .
.
解法二:以A为原点,以射线AB、AC、AA1分别为x、y、z的正半轴建立空间直角坐标系,设AB=AA1=AC=2a>0,可知各点坐标分别为

A(0,0,0),B(2a,0,0),C(0,2a,0),B1(2a,0,2a),E(0,2a,a),F(a,a,0),D(a,0,a)
(Ⅰ)![]() =(-a,2a,0),
=(-a,2a,0),
又因为(-a,2a,0)=a(-1,2,0),
即![]() =a(-1,2,0).
=a(-1,2,0).
∴![]() 与向量(-1,2,0)平行,设点G(-1,2,0),
与向量(-1,2,0)平行,设点G(-1,2,0),
则![]() =(-1,2,0)
=(-1,2,0)
∴![]() 与
与![]() 平行,而直线AG在平面ABC内,直线DE在平面ABC外,∴DE∥平面ABC.
平行,而直线AG在平面ABC内,直线DE在平面ABC外,∴DE∥平面ABC.
(Ⅱ)证明:![]() =(-a,a,-2a),
=(-a,a,-2a), ![]() =(a,-a,-a),
=(a,-a,-a),![]() =(a,a,0),
=(a,a,0),
∴![]() ·
·![]() =-a×a+a×(-a)+(-2a)×(-a)=0,
=-a×a+a×(-a)+(-2a)×(-a)=0,
![]() ·
·![]() =-a×a+a×a-2a×0=0,
=-a×a+a×a-2a×0=0,
∴![]() ⊥
⊥![]() ,
,![]() ⊥
⊥![]()
又AF∩EF=F,∴B1F⊥平面AEF.
(Ⅲ)由(Ⅱ)知,![]() =(-a,a,-2a)是平面AEF的一个法向量,设二面角B1-AE-F的大小为θ,根据已知得θ是锐角,设平面AEB1的一个法向量为n=(x,y,1),∵
=(-a,a,-2a)是平面AEF的一个法向量,设二面角B1-AE-F的大小为θ,根据已知得θ是锐角,设平面AEB1的一个法向量为n=(x,y,1),∵![]() =(0,2a,a),
=(0,2a,a), ![]() =(2a,0,2a),且
=(2a,0,2a),且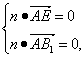
∴![]() 解得
解得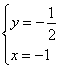 ,∴n=(-1,
,∴n=(-1,![]() ,1)
,1)
∴cosθ=![]()
∴θ=arcos=![]() ,
,
∴二面角B1-AE-F的大小为arcos![]() .
.

 如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.
如图,已知直三棱柱ABC-A1B1C1,∠ACB=90°,AC=BC=2,AA1=4.E、F分别是棱CC1、AB中点.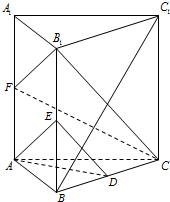 已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点.
已知直三棱柱ABC-A1B1C1的所有棱长都相等,且D,E,F分别为BC,BB1,AA1的中点. 如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点,
如图所示,已知直三棱柱ABC-A′B′C′,AC=AB=AA′=2,AC,AB,AA′两两垂直,E,F,H分别是AC,AB,BC的中点, 如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点.
如图,已知直三棱柱ABC-A1B1C1的侧棱长为2,底面△ABC是等腰直角三角形,且∠ACB=90°,AC=2,D是A A1的中点. 如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.
如图,已知直三棱柱ABC-A1B1C1中,AB=AC;M.N.P分别是棱BC.CC1.B1C1的中点.