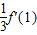题目内容
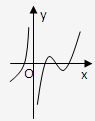
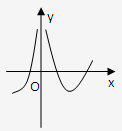
 设函数y=f(x)可导,y=f(x)的图象如图1所示,则导函数y=f′(x)可能为( )
设函数y=f(x)可导,y=f(x)的图象如图1所示,则导函数y=f′(x)可能为( )分析:先根据导函数的正负与原函数的单调性之间的关系,结合函数f(x)的单调性是先增后减再增,判断出f′(x)的值是先正后负再正,然后观察选项ABCD满足条件的只有D,得到答案.
解答:解:根据y=f(x)的图象可知其定义域为{x|x≠0},
故其导函数的定义域也为{x|x≠0},
又从原函数y=f(x)的图象可知,函数y=f(x)的单调性是:
函数y=f(x)在(-∞,0),(0,a)上是增函数,在(a,b)上是减函数,在(b,+∞)是增函数,
即y=f(x)是先增后减再增,
得出导函数是先正后负再正,
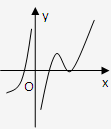
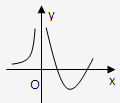
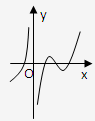
根据选项中的函数f(x)的单调性知选D.
故选D.
故其导函数的定义域也为{x|x≠0},
又从原函数y=f(x)的图象可知,函数y=f(x)的单调性是:
函数y=f(x)在(-∞,0),(0,a)上是增函数,在(a,b)上是减函数,在(b,+∞)是增函数,
即y=f(x)是先增后减再增,
得出导函数是先正后负再正,
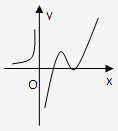
根据选项中的函数f(x)的单调性知选D.
故选D.
点评:本题主要考查导函数的正负与原函数的增减性的关系--导函数小于0时原函数单调递减,导函数大于0时原函数单调递增.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
设函数y=f(x)可导,则
等于( )
| lim |
| △x→0 |
| f(1+△x)-f(1) |
| 3△x |
| A、f'(1) | ||
| B、3f'(1) | ||
C、
| ||
| D、以上都不对 |
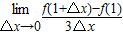 等于( )
等于( )