题目内容
在△ABC中,角A,B,C所对的边分别是a,b,c.己知csin A=  acos
C.
acos
C.
(I)求C;
(II)若c=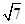 ,且
,且 求△ABC的面积.
求△ABC的面积.
【答案】
(Ⅰ)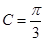 ;(Ⅱ)
;(Ⅱ)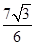 或
或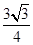
【解析】
试题分析:(Ⅰ)三角形问题中,涉及边角混合的式子,往往会根据正弦定理或者余弦定理边角转化,或转化为边的式子,利用代数方法处理;或转换为 角的方程,利用三角函数知识处理,该题利用正弦定理转化为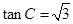 ,再求C;(Ⅱ)已知中含有三个角
,再求C;(Ⅱ)已知中含有三个角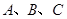 ,观察方程中有
,观察方程中有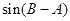 ,利用
,利用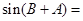
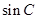 ,转化为两个角的三角方程
,转化为两个角的三角方程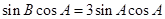 ,然后分
,然后分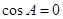 和
和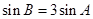 两种情况求三角形面积.
两种情况求三角形面积.
试题解析:(Ⅰ)由正弦定理,得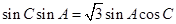 ,因为
,因为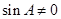 ,解得
,解得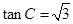 ,
,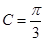 .
.
(Ⅱ)由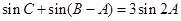 ,得
,得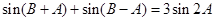 ,
,
整理,得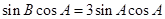 .
.
若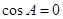 ,则
,则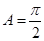 ,
,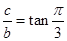 ,
,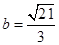 ,
,
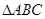 的面积
的面积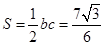
若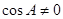 ,则
,则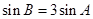 ,
,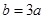 .
.
由余弦定理,得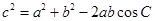 ,解得
,解得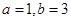 .
.
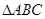 的面积
的面积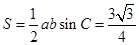 .综上,
.综上,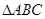 的面积为
的面积为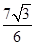 或
或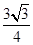 .
.
考点:1.正弦定理;2.余弦定理;3.三角形面积公式.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |