题目内容
已知函数 .
.
(1)若存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围;
的取值范围;
(2)设 ,证明:
,证明: .
.
(1)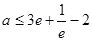 ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)这是一个含参不等式恒成立,求参数取值范围的问题,通常方法是根据函数性质进行求解,或分离参数转化为求函数最值问题,若方便分离参数又较容易求分离后函数的最值,还是分离参数较好,这样可避免对参数的讨论;(2)这是一个以函数的凹凸那条性为背景的一个不等式的证明问题双变元问题,可以将其中一个看成主元,另一个看成参数,构造函数 ,通过求导判断函数的单调性和最值达到证明的目的.
,通过求导判断函数的单调性和最值达到证明的目的.
试题解析:(1)(1)由 变形为
变形为 .
.
令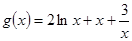 ,则
,则
故当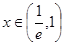 时,
时, ,
, 在
在 上单调递减;
上单调递减;
当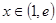 时,
时, ,
, 在
在 上单调递增,
上单调递增,
所以 的最大值只能在
的最大值只能在 或
或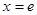 处取得
处取得
又 ,
,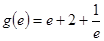 ,所以
,所以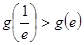
所以 ,从而
,从而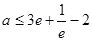 .
.
(2)∵ ,∴
,∴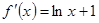
设 ,则
,则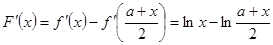
当 时,
时, ,
,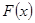 在
在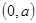 上为减函数;
上为减函数;
当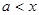 时,
时, ,
,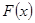 在
在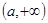 上为增函数.
上为增函数.
从而当 时,
时,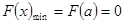 ,
,
因为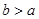 ,所以
,所以 .
.
考点:函数的零点、三角函数的性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, .
. ,是否存在
,是否存在 、
、 ,使
,使 为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由;
为偶函数,如果存在,请举例并证明你的结论,如果不存在,请说明理由; ,
, ,求
,求 在
在 上的单调区间;
上的单调区间; ,
, 对
对 ,,有
,,有 成立,求
成立,求 ,
, 恒过定点 (3,2).
恒过定点 (3,2).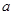 ;
; 的图象向下平移1个单位,再向左平移
的图象向下平移1个单位,再向左平移 ,设函数
,设函数 ,求
,求 ,若在其定义域内,不等式
,若在其定义域内,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围. .已知甲、乙两地相距100千米.
.已知甲、乙两地相距100千米. 且
且 .
. 的值;
的值; 在
在 上的单调性,并给予证明.
上的单调性,并给予证明. .
. 时,画出函数
时,画出函数 的简图,并指出
的简图,并指出 (其中
(其中 )的图象如图所示.
)的图象如图所示.
 的解析式;
的解析式; ,且
,且 ,求
,求 的单调区间.
的单调区间. 对任意
对任意 满足
满足 ,
, ,若当
,若当 时,
时, (
( 且
且 ),且
),且 .
. 的值;
的值; 的值域.
的值域. ,若在定义域内存在实数
,若在定义域内存在实数 ,满足
,满足 ,则称
,则称 ,试判断
,试判断 是定义在区间
是定义在区间 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数 的取值范围;
的取值范围; 为定义域
为定义域 上的“局部奇函数”,求实数
上的“局部奇函数”,求实数