题目内容
已知正项数列{an}中, .用数学归纳法证明:
.用数学归纳法证明: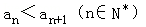 .
.
 .用数学归纳法证明:
.用数学归纳法证明: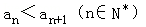 .
.证明:当n=1时,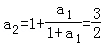 ,a1<a2,
,a1<a2,
所以n=1时,不等式成立.
假设n=k(k∈N*)时,ak<ak+1成立,
则n=k+1时,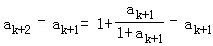
=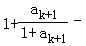
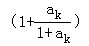
=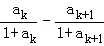
=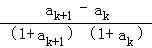 >0;
>0;
即ak+2﹣ak+1>0,
所以n=k+1时,不等式也成立.
综上所述,不等式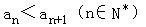 成立.
成立.
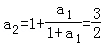 ,a1<a2,
,a1<a2,所以n=1时,不等式成立.
假设n=k(k∈N*)时,ak<ak+1成立,
则n=k+1时,
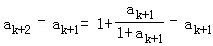
=
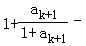
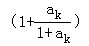
=
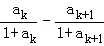
=
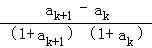 >0;
>0;即ak+2﹣ak+1>0,
所以n=k+1时,不等式也成立.
综上所述,不等式
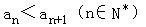 成立.
成立.
练习册系列答案
相关题目