Question

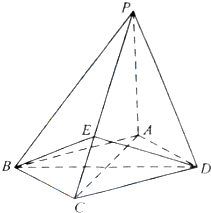如图，四棱锥P-ABCD中，底面ABCD为菱形，PA⊥底面ABCD，AC=2

2

，PA=2，E是PC上的一点，PE=2EC．
（Ⅰ）证明：PC⊥平面BED；
（Ⅱ）设二面角A-PB-C为90°，求PD与平面PBC所成角的大小．

Answer 1

分析：（I）先由已知建立空间直角坐标系，设D（

2

，b，0），从而写出相关点和相关向量的坐标，利用向量垂直的充要条件，证明PC⊥BE，PC⊥DE，从而利用线面垂直的判定定理证明结论即可；
（II）先求平面PAB的法向量，再求平面PBC的法向量，利用两平面垂直的性质，即可求得b的值，最后利用空间向量夹角公式即可求得线面角的正弦值，进而求得线面角

解答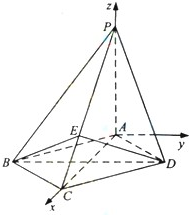：解：（I）以A为坐标原点，建立如图空间直角坐标系A-xyz，
设D（

2

，b，0），则C（2

2

，0，0），P（0，0，2），E（

4 2

3

，0，

2

3

），B（

2

，-b，0）
∴

PC

=（2

2

，0，-2），

BE

=（

2

3

，b，

2

3

），

DE

=（

2

3

，-b，

2

3

）
∴

PC

•

BE

=

4

3

-

4

3

=0，

PC

•

DE

=0
∴PC⊥BE，PC⊥DE，BE∩DE=E
∴PC⊥平面BED
（II）

AP

=（0，0，2），

AB

=（

2

，-b，0）
设平面PAB的法向量为

m

=（x，y，z），则

m • AP =2z=0 m • AB = 2 x-by=0

取

m

=（b，

2

，0）
设平面PBC的法向量为

n

=（p，q，r），则

n • PC =2 2 p-2r=0 n • BE = 2 3 p+bq+ 2 3 r=0

取

n

=（1，-

2

b

，

2

）
∵平面PAB⊥平面PBC，∴

m

•

n

=b-

2

b

=0．故b=

2

∴

n

=（1，-1，

2

），

DP

=（-

2

，-

2

，2）
∴cos＜

DP

，

n

＞=

n • DP

| n |•| DP  |

=

1

2

设PD与平面PBC所成角为θ，则sinθ=

1

2

∴θ=30°
∴PD与平面PBC所成角的大小为30°

点评：本题主要考查了利用空间直角坐标系和空间向量解决立体几何问题的一般方法，线面垂直的判定定理，空间线面角的求法，有一定的运算量，属中档题