题目内容
如图所示的曲线是以锐角△ABC的顶点B、C为焦点,且经过点A的双曲线,若△ABC的内角的对边分别为a,b,c,且 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )
A.

B.

C.

D.

【答案】分析:先根据 求得sinC,进而求得C,进而根据余弦定理求得c,最后通过离心率公式求得答案.
求得sinC,进而求得C,进而根据余弦定理求得c,最后通过离心率公式求得答案.
解答:解: ,
,
∵C为锐角,
∴C= ,由余弦定理知
,由余弦定理知 ,
,
 ,
, .
.
故选D
点评:本题主要考查双曲线的简单性质.离心率是圆锥曲线的一个重要特征量,是高考“经久不衰”的重点和热点内容,必须高度重视.本题以椭圆为载体,巧妙地将光的反射融于其中,对平面几何及解析几何的考查均非常深刻,对计算能力要求较高,极富思考性和挑战性,具有较好的区分和选拔功能.
 求得sinC,进而求得C,进而根据余弦定理求得c,最后通过离心率公式求得答案.
求得sinC,进而求得C,进而根据余弦定理求得c,最后通过离心率公式求得答案.解答:解:
 ,
,∵C为锐角,
∴C=
 ,由余弦定理知
,由余弦定理知 ,
, ,
, .
.故选D
点评:本题主要考查双曲线的简单性质.离心率是圆锥曲线的一个重要特征量,是高考“经久不衰”的重点和热点内容,必须高度重视.本题以椭圆为载体,巧妙地将光的反射融于其中,对平面几何及解析几何的考查均非常深刻,对计算能力要求较高,极富思考性和挑战性,具有较好的区分和选拔功能.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
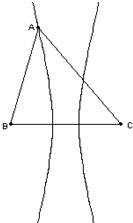 如图所示的曲线是以锐角△ABC的顶点B、C为焦点,且经过点A的双曲线,若△ABC的内角的对边分别为a,b,c,且a=4,b=6,
如图所示的曲线是以锐角△ABC的顶点B、C为焦点,且经过点A的双曲线,若△ABC的内角的对边分别为a,b,c,且a=4,b=6,| csinA |
| a |
| ||
| 2 |
A、
| ||||
B、
| ||||
C、3-
| ||||
D、3+
|
 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )




 ,则此双曲线的离心率为( )
,则此双曲线的离心率为( )




 ,则此双曲线的离心率为
,则此双曲线的离心率为 



