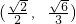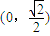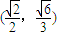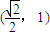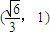题目内容
已知点D是等腰直角三角形△ABC的重心，B=| π |
| 2 |
| BP |
| BA |
| BC |
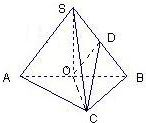
分析：以BA为x轴，BC为y轴，建立如图所示的直角坐标系．由
=x
+y
，得：P点的坐标为（x，y），P点在图中阴影部分的区域内，将原问题转化为z=2x+y，何时取最大值最小值问题解决即可．
| BP |
| BA |
| BC |
解答：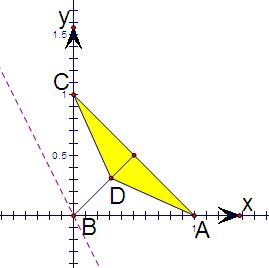
解：以BA为x轴，BC为y轴，建立如图所示的直角坐标系．
由
=x
+y
，得：P点的坐标为（x，y）
且P点在图中阴影部分的区域内，D（
，
）
直线z=2x+y
过点A时z取最大值，此时z=2，
当过点D时取得最小值，最小值为：1
故所求2x+y的取值范围为[1，2]，
故答案为：[1，2]．
解：以BA为x轴，BC为y轴，建立如图所示的直角坐标系．由
| BP |
| BA |
| BC |
且P点在图中阴影部分的区域内，D（
| 1 |
| 3 |
| 1 |
| 3 |
直线z=2x+y
过点A时z取最大值，此时z=2，
当过点D时取得最小值，最小值为：1
故所求2x+y的取值范围为[1，2]，
故答案为：[1，2]．
点评：在解决线性规划的题时，我们常用“角点法”，其步骤为：①由约束条件画出可行域?②求出可行域各个角点的坐标?③将坐标逐一代入目标函数?④验证，求出最优解．
练习册系列答案
相关题目
