题目内容
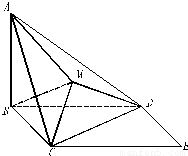
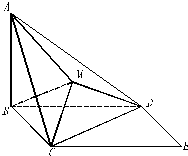 AB⊥平面BCED,
AB⊥平面BCED,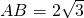 ,四边形BCED是边长为2的菱形,且∠DBC=60°,将△CDE沿CD折起,使平面BCD⊥平面MCD.
,四边形BCED是边长为2的菱形,且∠DBC=60°,将△CDE沿CD折起,使平面BCD⊥平面MCD.
(1)求点A到平面BMC的距离;
(2)求平面ACM与平面BCD所成二面角的正弦值.
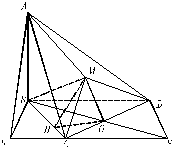 解:(1)如图,取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,…(1分)
解:(1)如图,取CD中点O,连OB,OM,则OB⊥CD,OM⊥CD,…(1分)又平面MCD⊥平面BCD,则MO⊥平面BCD,…(3分)
所以MO∥AB,…(4分)
所以A、B、O、M共面,
延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角,OB=MO=
 ,
,∵MO∥AB,∴MO∥面ABC,∴M、O到平面ABC的距离相等,…(6分)
作OH⊥BC于H,连接MH,则MH⊥BC,求得OH=OCsin60°=
 ,MH=
,MH= ,…(8分)
,…(8分)利用体积相等得,VA-MBC=VM-ABC,
∴
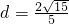 .…(10分)
.…(10分)(2)CE是平面ACM与平面BCD的交线,由(1)知,O是BE的中点,则BCED是菱形,
作BF⊥EC于F,连接AF,则AF⊥EC,所以∠AFB就是二面角A-EC-B的平面角,…(12分)
设∠AFB为θ,因为∠BCE=120°,所以∠BCF=60°,
所以BF=BC•sin60°=
 ,tanθ=
,tanθ= ,
,所以,所求二面角的正弦值是
 .…(14分)
.…(14分)分析:(1)取CD中点O,连OB,OM,可得MO∥AB,延长AM、BO相交于E,则∠AEB就是AM与平面BCD所成的角,OB=MO=
 ,可证M、O到平面ABC的距离相等,作OH⊥BC于H,连接MH,则MH⊥BC,利用体积相等,可得点A到平面BMC的距离;
,可证M、O到平面ABC的距离相等,作OH⊥BC于H,连接MH,则MH⊥BC,利用体积相等,可得点A到平面BMC的距离;(2)作BF⊥EC于F,连接AF,则AF⊥EC,所以∠AFB就是二面角A-EC-B的平面角,求出AB,BF的值,即可求二面角的正弦值.
点评:本题考查点到面的距离,考查面面角,解题的关键是利用等体积求点到面的距离,正确作出面面角,属于中档题.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥
如图所示的几何体是由以等边三角形ABC为底面的棱柱被平面DEF所截而得,已知FA⊥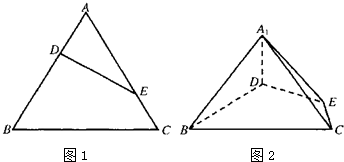
 AB⊥平面BCED,
AB⊥平面BCED,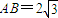 ,四边形BCED是边长为2的菱形,且∠DBC=60°,将△CDE沿CD折起,使平面BCD⊥平面MCD.
,四边形BCED是边长为2的菱形,且∠DBC=60°,将△CDE沿CD折起,使平面BCD⊥平面MCD.