题目内容
如图，在底面为平行四边形的四棱锥P-AB-CD，AB⊥AC，PA⊥平面ABCD且PA=AB，点E是PD的中点.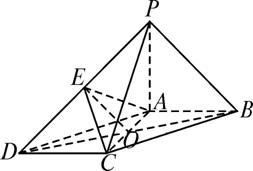
(1)求证：AC⊥PB；
(2)求证：PB∥平面AEC.
解析：(1)证明：∵PA⊥平面ABCD，
∴AB是PB在平面ABCD上的射影.
又∵AB⊥AC，AC
平面ABCD，
∴AC⊥PB.
(2)证明：连结BD，与AC相交于O，连结EO.
∵ABCD是平行四边形，
∴O是BD的中点.
又E是PD的中点，
∴EO∥PB.
又PB
平面AEC，EO
平面AEC，
∴PB∥平面AEC.
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且PA=AB，点E是PD的中点．
如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，且 PA=AB=AC=2，点E是PD的中点．
如图，在底面为平行四边形的四棱柱ABCD-A1B1C1D1中，D1D⊥底面ABCD，AD=1，CD=2，∠DCB=60°．
如图，在底面为平行四边形的四棱柱ABCD-A1B1C1D1中，D1D⊥底面ABCD，AD=1，CD=2，∠DCB=60°．