题目内容
在下列区间中，函数f（x）=ex+4x-3的零点所在的区间为（ ）A．（-
，0）B．（0，
）C．（
，
）D．（
，
）
【答案】分析：分别计算出f（0）、f（1）、f（
）、f（
）的值，判断它们的正负，再结合函数零点存在性定理，可以得出答案．
解答：解：∵f（0）=e-3=-2＜0 f（1）=e1+4-3＞0
∴根所在的区间x∈（0，1）排除A选项
又∵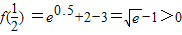
∴根所在的区间x∈（0，
），排除D选项
最后计算出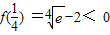
，
，
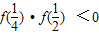得出选项C符合；
故选C．
点评：e=2.71828…是一个无理数，本题计算中要用到
等的值，对计算有一定的要求．
）、f（）的值，判断它们的正负，再结合函数零点存在性定理，可以得出答案．解答：解：∵f（0）=e-3=-2＜0 f（1）=e1+4-3＞0
∴根所在的区间x∈（0，1）排除A选项
又∵
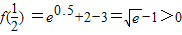
∴根所在的区间x∈（0，
），排除D选项最后计算出
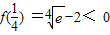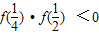，，得出选项C符合；
故选C．
点评：e=2.71828…是一个无理数，本题计算中要用到
等的值，对计算有一定的要求． 
练习册系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
在下列区间中，函数f（x）=3x-x2有零点的区间是（ ）
| A、[0，1] | B、[1，2] | C、[-2，-1] | D、[-1，0] |