题目内容
若loga2<logb2<0,则( )
| A.0<a<b<1 | B.0<b<a<1 | C.a>b>1 | D.b>a>1 |
∵loga2<logb2<0,
由对数换底公式得:
∴
<
<0
∴0>log2a>log2b
∴根据对数的性质得:
∴0<b<a<1.
故选B.
由对数换底公式得:
∴
| 1 |
| log2a |
| 1 |
| log2b |
∴0>log2a>log2b
∴根据对数的性质得:
∴0<b<a<1.
故选B.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目

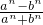 =1(其中n∈N+);
=1(其中n∈N+);
 =1(其中n∈N+);
=1(其中n∈N+);