题目内容
已知 ,且
,且 ,
, .
.
(1)求cosα的值;
(2)证明: .
.
解:(1) =
= …(6分)
…(6分)
(2)证明:因为 易得
易得 ,
,
又 所以
所以 ,…(8分)
,…(8分)
由(1)可得sinα= ,
,
所以 …(10分)
…(10分)
分析:(1)直接利用二倍角的余弦函数,以及三角函数的平方关系,转化为 ,即可求解cosα.
,即可求解cosα.
(2)求出α+β的正弦与余弦值,利用(1)求出α的正弦函数值,求出cosβ的值,即可证明结果.
点评:本题考查二倍角的余弦函数,同角三角函数的基本关系式的应用,考查整体思想与计算能力.
 =
= …(6分)
…(6分)(2)证明:因为
 易得
易得 ,
,又
 所以
所以 ,…(8分)
,…(8分)由(1)可得sinα=
 ,
,所以
 …(10分)
…(10分)分析:(1)直接利用二倍角的余弦函数,以及三角函数的平方关系,转化为
 ,即可求解cosα.
,即可求解cosα.(2)求出α+β的正弦与余弦值,利用(1)求出α的正弦函数值,求出cosβ的值,即可证明结果.
点评:本题考查二倍角的余弦函数,同角三角函数的基本关系式的应用,考查整体思想与计算能力.

练习册系列答案
相关题目
 的定义域是
的定义域是 ,且对任意的正实数
,且对任意的正实数 都有
都有 恒成立. 已知
恒成立. 已知 ,且
,且 时,
时, .
. 的值K]
的值K] 在
在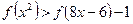 .
. ,且函数
,且函数 ,
,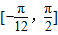 上的最大、最小值及相应的x值;
上的最大、最小值及相应的x值; 是公比
是公比 大于1的等比数列,
大于1的等比数列, 为数列
为数列 项和,已知
项和,已知 ,且
,且 构成等差数列.
构成等差数列. ,求数列
,求数列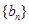 的前
的前 .
. 且
且 ,函数
,函数 (1)求函数
(1)求函数 的最小正周期及单调递增区间;
的最小正周期及单调递增区间; ,分别求
,分别求 及
及 的值
的值 的定义域是
的定义域是 ,且对任意的正实数
,且对任意的正实数 都有
都有 恒成立. 已知
恒成立. 已知 ,且
,且 时,
时, .
. 的值K]
的值K] 在
在 .
.