题目内容
已知定点0(0,0)、F(0,2),动点T(t,8),动点Q满足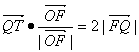
(Ⅰ)求动点Q的轨迹方程;
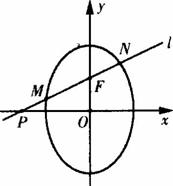
(Ⅱ)过点F(0,2)的直线l与点Q的轨迹交于M(x1,y1),、N(x2,y2)两点,与x轴交于点p.若![]() 分别用y1、y2表示出
分别用y1、y2表示出![]() 1、
1、![]() 2,并求
2,并求![]() 1+
1+![]() 2的值.
2的值.
解:(Ⅰ)令Q(x,y),则![]() =(t-z,8-y),
=(t-z,8-y),![]() (x,y-2).
(x,y-2).
由已知,![]() =(0,1).∵
=(0,1).∵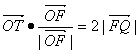 ,∴8-y=
,∴8-y=![]() ,
,
∴(8-y)2=4x2+4(y-2)2,∴![]() =1.
=1.
∴点Q的轨迹方程为![]() =1.
=1.
(Ⅱ)设直线l的方程为y=kx+2.
由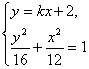 消去x,有3y2+
消去x,有3y2+![]() =48.
=48.
即(4+3k2)y2-16y+16-48k2=0.
∵M(x1,y1),N(x2,y2),则y1+y2=![]() ;y1y2=
;y1y2=![]() .
.
由![]() +λ1
+λ1![]() ,∴λ1=
,∴λ1=![]() ,λ2=
,λ2=![]()
λ1+λ2=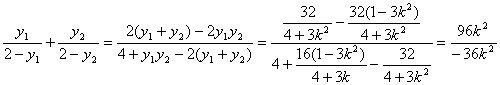
![]() 。
。

练习册系列答案
相关题目
 已知椭圆
已知椭圆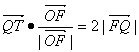 .
.