题目内容

抛物线的顶点在原点O，焦点为椭圆
x2
3
+
y2
2
=1的右焦点F．
（1）求抛物线的方程；
（2）设点P在抛物线上运动，求P到直线y=x+3的距离的最小值，并求此时点P的坐标．
（1）由题知F（1，0）
∴抛物线方程：y2=4x．
（2）解法1：设P（x，y），
则P到直线y=x+3的距离d=
|x-y+3|
2
，又y2=4x
∴d=
|
y2
4
-y+3|
2
=
|y2-4y+12|
4
2
=
(y-2)2+8
4
2
≥
8
4
2
=
2
．
∴当P（1，2）时，dmin=
2
．
解法2：设l与直线y=x+3平行且与抛物线相切，
即l：y=x+b，由
y=x+b
y2=4x

得x2+（2b-4）x+b2=0，∵△=（2b-4）2-4b2=0，∴b=1
此时切点P（1，2），P到直线y=x+3的距离最小为
|3-1|
2
=
2
．
练习册系列答案
相关题目
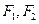设为椭圆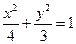左、右焦点，过椭圆中心任作一条直线与椭圆交于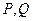两点，当四边形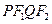面积最大时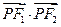，的值等于         .               
椭圆C：
x2
9
+
y2
4
=1，斜率为k的直线l与椭圆相交于点M，N，点A是线段MN的中点，直线OA（O为坐标原点）的斜率是k′，那么kk′=______．
在平面直角坐标系xOy中，已知椭圆E：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
1
2
，一条准线方程为x=4．
（1）求椭圆E的标准方程；
（2）若点A，B分别是椭圆E的左、右顶点，直线l经过点B且垂直于x轴，点P是椭圆上异于A，B的任意一点，直线AP交l于点M，设直线OM的斜率为k1，直线BP的斜率为k2，求证：k1k2为定值．
已知平面直角坐标系xoy中的一个椭圆，它的中心在原点，左焦点为F(-
3
，0)，右顶点为D（2，0），设点A（1，
1
2
）．
（1）求该椭圆的标准方程；
（2）若P是椭圆上的动点，求线段PA的中点M的轨迹方程；
（3）过原点O的直线交椭圆于B，C两点，求△ABC面积的最大值，并求此时直线BC的方程．
设抛物线y2=2px（p为常数）的准线与X轴交于点K，过K的直线l与抛物线交于A、B两点，则
OA
•
OB
=______．
若动圆过定点A（-3，0）且和定圆（x-3）2+y2=4外切，则动圆圆心P的轨迹为（　　）
A．双曲线B．椭圆C．抛物线D．双曲线一支
若直线y=-x+m与曲线y=
5-
1
4
x2
只有一个公共点，则m的取值范围是（　　）
A．-1≤m＜2B．-2
5
≤m≤2
5
C．-2≤m＜2或m=5D．-2
5
≤m≤2
5
或m=5
已知两点M（-1，0）、N（1，0），动点P（x，y）满足|
MN
|•|
NP
|-
MN
•
MP
=0，
（1）求点P的轨迹C的方程；
（2）假设P1、P2是轨迹C上的两个不同点，F（1，0），λ∈R，
FP1
=λ
FP2
，求证：
1
|FP1|
+
1
|FP2|
=1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网