题目内容
椭圆
+
=1上的点到直线2x-y=7距离最近的点的坐标为( )
| x2 |
| 2 |
| y | 2 |
分析:设与直线2x-y=7平行且与椭圆
+
=1相切的直线l的方程为:2x-y=t,与椭圆的方程联立化为关于x的一元二次方程,令△=0,进而解出点的坐标.
| x2 |
| 2 |
| y | 2 |
解答:解:设与直线2x-y=7平行且与椭圆
+
=1相切的直线l的方程为:2x-y=t,
联立
,化为9x2-8tx+2t2-2=0.(*)
∴△=64t2-36(2t2-2)=0,化为t2=9,解得t=±3.
取t=3,代入(*)可得:9x2-24x+16=0,解得x=
,∴y=2×
-3=-
.
∴椭圆
+
=1上的点到直线2x-y=7距离最近的点的坐标为(
,-
).
故选B.
| x2 |
| 2 |
| y | 2 |
联立
|
∴△=64t2-36(2t2-2)=0,化为t2=9,解得t=±3.
取t=3,代入(*)可得:9x2-24x+16=0,解得x=
| 4 |
| 3 |
| 4 |
| 3 |
| 1 |
| 3 |
∴椭圆
| x2 |
| 2 |
| y | 2 |
| 4 |
| 3 |
| 1 |
| 3 |
故选B.
点评:本题考查了直线与椭圆相切问题转化为方程联立得到△=0、相互平行的直线之间的斜率公式等基础知识与基本技能方法,属于中档题.

练习册系列答案
相关题目
 (2011•嘉定区三模)如图,已知椭圆
(2011•嘉定区三模)如图,已知椭圆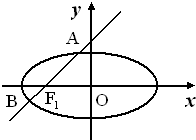 过椭圆
过椭圆