题目内容
若方程x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点(xi,
)(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是
| 9 | xi |
a>24或a<-24
a>24或a<-24
.分析:原方程等价于x3+a=
,原方程的实根是曲线y=x3+a与曲线y=
的交点的横坐标,分别作出左右两边函数的图象:分a>0与a<0讨论,可得答案.
| 9 |
| x |
| 9 |
| x |
解答:解:解:方程的根显然x≠0,原方程等价于x3+a=
,
原方程的实根是曲线y=x3+a与曲线y=
,的交点的横坐标,
而曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的,
若交点(xi,
)(i=1,2,…,k)均在直线y=x的同侧,
因直线y=x与y=
交点为:(-3,-3),(3,3),
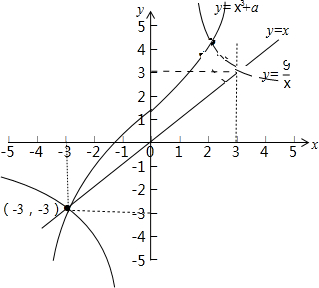
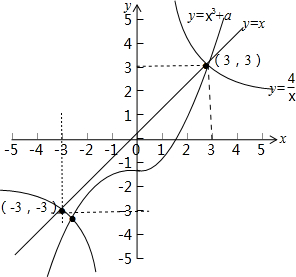
所以结合图象可得:
或
,也即a>(-x3-3)max,(x<-3)或a<(3-x3)min,(x>3)
解得,a>24或a<-24,
故答案为:a>24或a<-24;
| 9 |
| x |
原方程的实根是曲线y=x3+a与曲线y=
| 9 |
| x |
而曲线y=x3+a是由曲线y=x3向上或向下平移|a|个单位而得到的,
若交点(xi,
| 9 |
| xi |
因直线y=x与y=
| 9 |
| x |

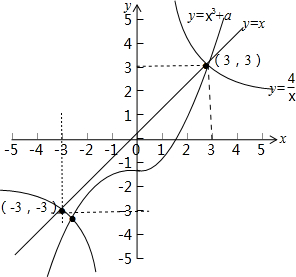
所以结合图象可得:
|
|
解得,a>24或a<-24,
故答案为:a>24或a<-24;
点评:本题综合考查了反比例函数,反比例函数与一次函数图象的交点问题,数形结合是数学解题中常用的思想方法,能够变抽象思维为形象思维,有助于把握数学问题的本质

练习册系列答案
相关题目
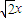 -1=0的解可视为函数y=x+
-1=0的解可视为函数y=x+ 的图象与函数y=
的图象与函数y=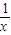 的图象交点的横坐标.若x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点
的图象交点的横坐标.若x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点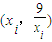 (i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .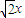 -1=0的解可视为函数y=x+
-1=0的解可视为函数y=x+ 的图象与函数y=
的图象与函数y=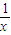 的图象交点的横坐标.若x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点
的图象交点的横坐标.若x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点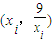 (i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 . -1=0的解可视为函数y=x+
-1=0的解可视为函数y=x+ 的图象与函数y=
的图象与函数y= 的图象交点的横坐标.若x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点
的图象交点的横坐标.若x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点 (i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .