题目内容
已知集合Sn={X|X=（x1，x2，…，xn），xi∈{0，1} ，i=1，2，…，n}（n≥2）。对于A=（a1，a2，…，an），B=（b1，b2，…，bn）∈Sn，定义A与B的差为A-B=（|a1-b1|，|a2-b2|，…，|an-bn|）；A与B之间的距离为d（A，B）=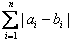
。
（1）证明：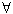
A，B，C∈Sn，有A-B∈Sn，且d（A-C，B-C）=d（A，B）；
（2）证明：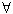
A，B，C∈Sn，d（A，B），d（A，C），d（B，C）三个数中至少有一个是偶数；
（3）设P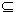
Sn，P中有m（m≥2）个元素，记P中所有两元素间距离的平均值为
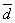（P），证明：
。
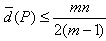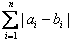。（1）证明：
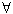A，B，C∈Sn，有A-B∈Sn，且d（A-C，B-C）=d（A，B）；（2）证明：
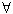A，B，C∈Sn，d（A，B），d（A，C），d（B，C）三个数中至少有一个是偶数；（3）设P
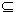Sn，P中有m（m≥2）个元素，记P中所有两元素间距离的平均值为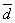（P），证明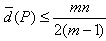：。解：（1）设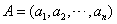
，
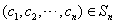，C=
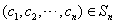
因为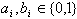
所以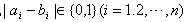
从而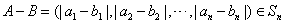
又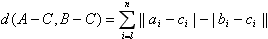
由题意知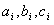
∈{0，1}（i=1，2，…n）
当ci=0时，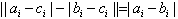
当ci=1时，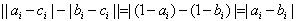
所以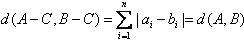
；
（2）设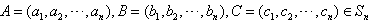
d（A，B）=k，d（A，C）=l，d（B，C）=h，
记O=（0，0，…，0）∈Sn，由（1）知
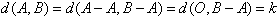
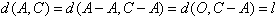
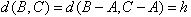
所以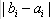
（i=1，2，…，n）中1的个数为k
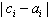（i=1，2，…，n）中1的个数为l
设t是使成立的i的个数，则h=l+k-2t，由此可知，k，l，h三个数不可能都是奇数，即d（A，B），d（A，C），d（B，C）三个数中至少有一个是偶数；
（3）
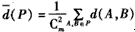，其中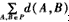
表示P中所有两个元素间距离的总和
设P中所有元素的第i个位置的数字中共有ti个1，m-ti个0
则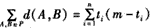
由于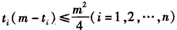
所以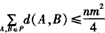
从而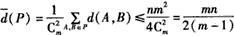
。
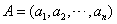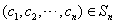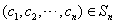
，，C=因为
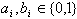
所以
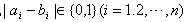
从而
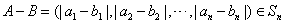
又
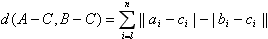
由题意知
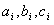∈{0，1}（i=1，2，…n）当ci=0时，
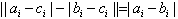
当ci=1时，
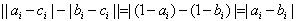
所以
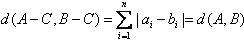；（2）设
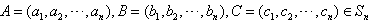
d（A，B）=k，d（A，C）=l，d（B，C）=h，
记O=（0，0，…，0）∈Sn，由（1）知
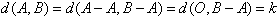
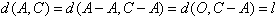
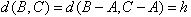
所以
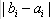（i=1，2，…，n）中1的个数为k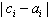（i=1，2，…，n）中1的个数为l设t是使成立的i的个数，则h=l+k-2t，由此可知，k，l，h三个数不可能都是奇数，即d（A，B），d（A，C），d（B，C）三个数中至少有一个是偶数；
（3）
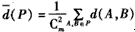，其中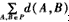表示P中所有两个元素间距离的总和设P中所有元素的第i个位置的数字中共有ti个1，m-ti个0
则
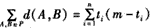
由于
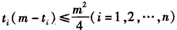
所以
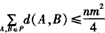
从而
。
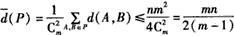练习册系列答案
相关题目
