题目内容
如图,已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
=
=λ(0<λ<1).若平面BEF⊥平面ACD,则λ的值为______.
| AE |
| AC |
| AF |
| AD |

∵AB⊥平面BCD,∴AB⊥CD,
∵CD⊥BC且AB∩BC=B,∴CD⊥平面ABC
又∵
=
=λ(0<λ<1),
∴不论λ为何值,恒有EF∥CD,
∴EF⊥平面ABC,BE?平面ABC,
∴BE⊥EF,
又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴BD=
,AB=
tan60°=
∴AC=
,
由AB2=AE?AC得AE=
故当λ=
=
时,平面BEF⊥平面ACD
故答案为:
∵CD⊥BC且AB∩BC=B,∴CD⊥平面ABC
又∵
| AE |
| AC |
| AF |
| AD |
∴不论λ为何值,恒有EF∥CD,
∴EF⊥平面ABC,BE?平面ABC,
∴BE⊥EF,
又平面BEF⊥平面ACD,
∴BE⊥平面ACD,∴BE⊥AC
∵BC=CD=1,∠BCD=90°,∠ADB=60°,
∴BD=
| 2 |
| 2 |
| 6 |
∴AC=
| 7 |
由AB2=AE?AC得AE=
| 6 | ||
|
故当λ=
| AE |
| AC |
| 6 |
| 7 |
故答案为:
| 6 |
| 7 |

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
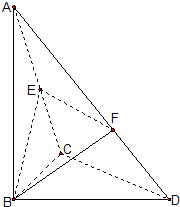 如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,
如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,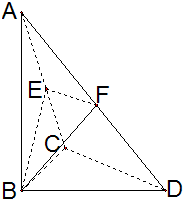 如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=CD=1,
如图,已知△BCD中,∠BCD=90°,AB⊥平面BCD,BC=CD=1,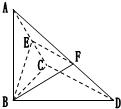 如图,已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
如图,已知△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且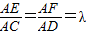 (0<λ<1).若平面BEF⊥平面ACD,则λ的值为 .
(0<λ<1).若平面BEF⊥平面ACD,则λ的值为 .
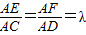 (0<λ<1).若平面BEF⊥平面ACD,则λ的值为 .
(0<λ<1).若平面BEF⊥平面ACD,则λ的值为 .