题目内容
在△ABC中,角A,B,C所对应的边分别为a,b,c且4sin2 -cos2C=
-cos2C= .
.
(Ⅰ)求角C的大小;
(Ⅱ)求sinA+sinB的最大值.
解:∵A,B,C为三角形的内角∴A+B+C=π
∵ ∴
∴
∴
即 ∴
∴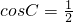
∵0<C<π∴
(II)由(I)得
∴
= =
=
当 时即
时即 sinA+sinB取得最大值
sinA+sinB取得最大值
分析:由三角形的内角和公式及二倍角公式可得,4sin2 -cos2C=
-cos2C= ,从而可得
,从而可得 解方程可求 cosC,进而求C;
解方程可求 cosC,进而求C;
(II)由(I)得 代入可得,
代入可得, ,化简可得其结果为
,化简可得其结果为 ,利用正弦函数的性质可求出答案.
,利用正弦函数的性质可求出答案.
点评:本题主要考查了利用二倍角公式对三角函数式进行化简、求值,还考查了辅助角公式的应用及正弦函数的 性质的应用,属于基础知识的简单综合运用,属于中档试题.
∵
 ∴
∴
∴

即
 ∴
∴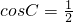
∵0<C<π∴

(II)由(I)得

∴

=
 =
=
当
 时即
时即 sinA+sinB取得最大值
sinA+sinB取得最大值
分析:由三角形的内角和公式及二倍角公式可得,4sin2
 -cos2C=
-cos2C= ,从而可得
,从而可得 解方程可求 cosC,进而求C;
解方程可求 cosC,进而求C;(II)由(I)得
 代入可得,
代入可得, ,化简可得其结果为
,化简可得其结果为 ,利用正弦函数的性质可求出答案.
,利用正弦函数的性质可求出答案.点评:本题主要考查了利用二倍角公式对三角函数式进行化简、求值,还考查了辅助角公式的应用及正弦函数的 性质的应用,属于基础知识的简单综合运用,属于中档试题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |