题目内容
设f(x)是上的奇函数,f(x+2)=-f(x),当x∈[0,1]时f(x)=x则f(-8.5)的值是
-0.5
-0.5
.分析:先由f(x+2)=-f(x),得出函数的周期,然后利用奇偶性求f(-8.5).
解答:解:由f(x+2)=-f(x),得f(x+4)=f(x),即函数f(x)的周期是4.
所以f(-8.5)=f(-0.5),因为f(x)是上的奇函数,
所以f(-8.5)=f(-0.5)=-f(0.5)=-0.5.
故答案为:-0.5.
所以f(-8.5)=f(-0.5),因为f(x)是上的奇函数,
所以f(-8.5)=f(-0.5)=-f(0.5)=-0.5.
故答案为:-0.5.
点评:本题主要考查函数奇偶性和周期性质的应用,要求熟练掌握函数性质的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
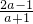 ,则a的取值范围是________.
,则a的取值范围是________. ,则a的取值范围是 .
,则a的取值范围是 . 为R上的1高调函数;
为R上的1高调函数;