Question

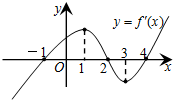（2011•蓝山县模拟）图为定义在R上的函数f（x）的导函数f'（x）的大致图象，则函数f（x）的单调递增区间为

（-1，2），（4，+∞）

，f（x）的极大值点为x=

2

．

Answer 1

分析：根据导函数的图象可知，函数在（-1，2），（4，+∞）上，导数大于0，在（2，4）上导数小于0，由此可得f（x）的单调递增区间与单调递减区间，从而可得函数的极大值点．

解答：解：根据导函数的图象可知，函数在（-1，2），（4，+∞）上，导数大于0，在（2，4）上导数小于0
∴f（x）的单调递增区间为（-1，2），（4，+∞），f（x）的单调递减区间为（2，4）
∴x=2时，f（x）取得极大值
∴f（x）的极大值点为x=2
故答案为：（-1，2），（4，+∞）；2

点评：本题重点考查函数的极值，考查导函数与函数单调性的关系，考查数形结合的数学思想，属于基础题．