题目内容
函数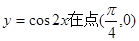 处的切线方程是( )
处的切线方程是( )
A.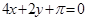 | B.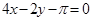 |
C.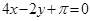 | D.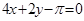 |
D
解析试题分析: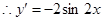 ,切线的斜率
,切线的斜率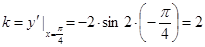 ,因此直线的点斜式方程
,因此直线的点斜式方程 ,化简得
,化简得 .
.
考点:利用导数的几何意义求切线方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数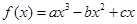 的图象如图所示,且
的图象如图所示,且 在
在 与
与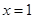 处取得极值,给出下列判断:
处取得极值,给出下列判断: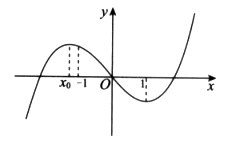
①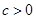 ;
;
②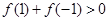 ;
;
③函数 在区间
在区间 上是增函数。
上是增函数。
其中正确的判断是( )
| A.①③ | B.② | C.②③ | D.①② |
函数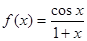 在
在 处的切线方程是( )
处的切线方程是( )
A.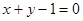 | B.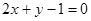 |
C. | D.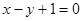 |
若f(x)=x2-2x-4ln x,则f′(x)>0的解集为( )
| A.(0,+∞) | B.(-1,0)∪(2,+∞) |
| C.(2,+∞) | D.(-1,0) |
曲线 在横坐标为
在横坐标为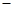 l的点处的切线为
l的点处的切线为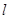 ,则点P(3,2)到直线
,则点P(3,2)到直线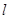 的距离为( )
的距离为( )
A.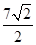 | B.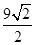 | C.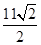 | D.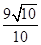 |
若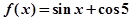 ,则该函数在点
,则该函数在点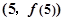 处切线的斜率等于( )
处切线的斜率等于( )
A.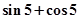 | B.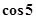 | C.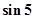 | D.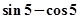 |
 的反函数为
的反函数为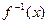 ,
, .
. ,求
,求 的取值范围D;
的取值范围D;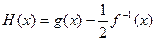 ,当
,当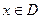 时,求函数
时,求函数 的值域.
的值域.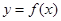 的图象如图1所示,则
的图象如图1所示,则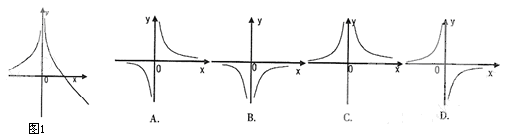
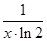 ;③(ex)′=ex;④(
;③(ex)′=ex;④(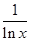 )′=x;⑤(x·ex)′=ex+1.
)′=x;⑤(x·ex)′=ex+1.