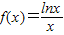题目内容

设a＞0,A={x||x-a|＜a+,x∈Z,B={x||x|＜2a,x∈Z,求A∩B.

试题答案

相关练习册答案

解:A={x|-a-＜x-a＜a+,x∈Z

={x|-＜x＜2a+,x∈Z,

B={x|-2a＜x＜2a,x∈Z.

(1)若-2a=-,即a=,则A∩B={x|-＜x＜,x∈Z；

(2)若0＜a＜,则A∩B={x|-2a＜x＜2a,x∈Z；

(3)若a＞,则A∩B={x|-＜x＜2a,x∈Z}.

深化升华

这是含有参数a的两个集合,求这两个集合的交集,应就a的情况进行讨论.这正体现了分类讨论的解题思想.

分类讨论思想即是根据解题的实际需要,有时需要对解题过程的某一环节分类讨论.分类讨论要注意“起点”的寻找和“层次的划分,做到“起点”讨论合理、自然,“层次”划分明确、清晰.分类讨论的原则是“既不重复,也不遗漏.”

练习册系列答案

本土寒假云南人民出版社系列答案

寒假作业南方日报出版社系列答案

1加1阅读好卷系列答案

专项复习训练系列答案

初中语文教与学阅读系列答案

阅读快车系列答案

完形填空与阅读理解周秘计划系列答案

英语阅读理解150篇系列答案

奔腾英语系列答案

标准阅读系列答案

相关题目

已知函数f(x)=

（1）求函数f（x）的单调区间；
（2）设a＞0，求函数f（x）在[2a，4a]上的最小值；
（3）某同学发现：总存在正实数a、b（a＜b），使a^b=b^a，试问：他的判断是否正确？若不正确，请说明理由；若正确，请直接写出a的取值范围（不需要解答过程）．

已知函数 $数学公式$
（1）求函数f（x）的单调区间；
（2）设a＞0，求函数f（x）在[2a，4a]上的最小值；
（3）某同学发现：总存在正实数a、b（a＜b），使a^b=b^a，试问：他的判断是否正确？若不正确，请说明理由；若正确，请直接写出a的取值范围（不需要解答过程）．

设a＞0,f(x)=ax²+bx+c,曲线y=f(x)在点P(x₀,f(x₀))处切线的倾斜角的取值范围为［0,

］,则P到曲线y=f(x)对称轴距离的取值范围为（）

A.［0,］ B.［0,］

C.［0,||］ D.［0,||］

（1）求函数f（x）的单调区间；
（2）设a＞0，求函数f（x）在[2a，4a]上的最小值；
（3）某同学发现：总存在正实数a、b（a＜b），使a^b=b^a，试问：他的判断是否正确？若不正确，请说明理由；若正确，请直接写出a的取值范围（不需要解答过程）．