题目内容
方程(a2+1)x2-2ax-3=0的两根x1,x2满足|x2|<x1(1-x2)且0<x1<1,则实数a的取值范围是( )
A.(1,
| B.(1+
| ||||||||
C.(-
| D.(-
|
∵|x2|<x1(1-x2),∴x1(1-x2)>0,又∵0<x1<1,∴x2<1
设f(x)=(a2+1)x2-2ax-3,∵方程有两根,∴△=4a2+12(a2+1)>0恒成立,
则f(1)=a2-2a-2>0,解得a>1+
或a<1-
;
∵f(0)=-3,∴x2<0<x1<1,
则|x2|<x1(1-x2)可化简为:x1+x2>x1x2,利用韦达定理得
>-
解得a>-
.
∴实数a的取值范围是:(-
,1-
)∪(1+
,+∞)
故选C.
设f(x)=(a2+1)x2-2ax-3,∵方程有两根,∴△=4a2+12(a2+1)>0恒成立,
则f(1)=a2-2a-2>0,解得a>1+
| 3 |
| 3 |
∵f(0)=-3,∴x2<0<x1<1,
则|x2|<x1(1-x2)可化简为:x1+x2>x1x2,利用韦达定理得
| 2a |
| a2+1 |
| 3 |
| a2+1 |
解得a>-
| 3 |
| 2 |
∴实数a的取值范围是:(-
| 3 |
| 2 |
| 3 |
| 3 |
故选C.

练习册系列答案
相关题目
方程(a2+1)x2-2ax-3=0的两根x1,x2满足|x2|<x1(1-x2)且0<x1<1,则实数a的取值范围是( )
A、(1,
| ||||||
B、(1+
| ||||||
C、(-
| ||||||
D、(-
|
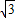 )
)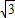 ,+∞)
,+∞) ,1-
,1-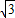 )∪(1+
)∪(1+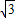 ,+∞)
,+∞) ,+∞)
,+∞)