题目内容
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.(I)求证:EF∥平面ADD1A1;
(Ⅱ)求二面角D-EF-A的余弦值.
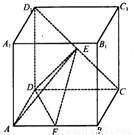
【答案】分析:(I)取DD1的中点G,连接GA,GE,推导出四边形AFEG为平行四边形,由此能够证明EF∥平面ADD1A1.
(Ⅱ)以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,分别求出平面DEF和平面AEF的法向量,利用向量法能够求出二面角D-EF-A的余弦值.
解答:(I)证明:如图,取DD1的中点G,连接GA,GE,
正方体ABCD-A1B1C1D1中,E、F分别是D1C、AB的中点,
∴GE∥DC∥AB,GE=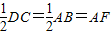 ,
,
∴GE∥AF,GE=AF,四边形AFEG为平行四边形,
∴EF∥AG,AG?平面ADD1A1,EF?平面ADD1A1,
∴EF∥平面ADD1A1.
(Ⅱ)解:如图,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,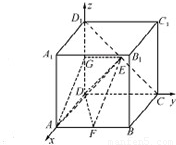
设棱长为2,则D(0,0,0),E(0,1,1),F(2,1,0),A(2,0,0),
∴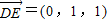 ,
,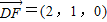 ,
,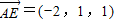 ,
,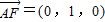 ,
,
设平面DEF的法向量为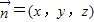 ,则
,则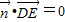 ,
,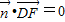 ,
,
∴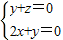 ,解得
,解得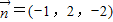 ,
,
设平面AEF的法向量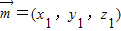 ,则
,则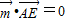 ,
,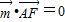 ,
,
∴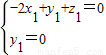 ,解得
,解得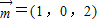 ,
,
设二面角D-EF-A的平面角为θ,
则cosθ=|cos<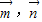 >|=|
>|=|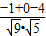 |=
|=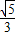 .
.
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,仔细解答,注意向量法和等价转化思想的合理运用.
(Ⅱ)以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,分别求出平面DEF和平面AEF的法向量,利用向量法能够求出二面角D-EF-A的余弦值.
解答:(I)证明:如图,取DD1的中点G,连接GA,GE,
正方体ABCD-A1B1C1D1中,E、F分别是D1C、AB的中点,
∴GE∥DC∥AB,GE=
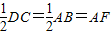 ,
,∴GE∥AF,GE=AF,四边形AFEG为平行四边形,
∴EF∥AG,AG?平面ADD1A1,EF?平面ADD1A1,
∴EF∥平面ADD1A1.
(Ⅱ)解:如图,以DA为x轴,以DC为y轴,以DD1为z轴,建立空间直角坐标系,

设棱长为2,则D(0,0,0),E(0,1,1),F(2,1,0),A(2,0,0),
∴
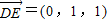 ,
,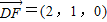 ,
,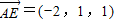 ,
,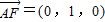 ,
,设平面DEF的法向量为
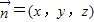 ,则
,则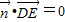 ,
,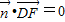 ,
,∴
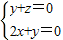 ,解得
,解得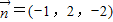 ,
,设平面AEF的法向量
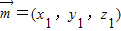 ,则
,则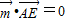 ,
,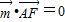 ,
,∴
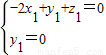 ,解得
,解得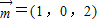 ,
,设二面角D-EF-A的平面角为θ,
则cosθ=|cos<
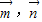 >|=|
>|=|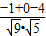 |=
|=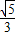 .
.点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,仔细解答,注意向量法和等价转化思想的合理运用.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )
8、如图,已知正方体ABCD-A1B1C1D1的棱长为3,点E,F在线段AB上,点M在线段B1C1上,点N在线段C1D1上,且EF=1,D1N=x,AE=y,M是B1C1的中点,则四面体MNEF的体积( )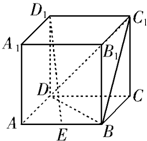 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点E为棱AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,E、F分别是D1C、AB的中点. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,点P,Q,R分别是棱AB,CC1,D1A1的中点. (2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.
(2012•宝山区一模)如图,已知正方体ABCD-A1B1C1D1 的棱长为2,E,F分别是BB1,CD的中点.