题目内容
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是p,电流能通过T4的概率是0.9.电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
(1)求p;
(2)求电流能在M与N之间通过的概率;
(3)ξ表示T1,T2,T3,T4中能通过电流的元件个数,求ξ的期望.
(1)求p;
(2)求电流能在M与N之间通过的概率;
(3)ξ表示T1,T2,T3,T4中能通过电流的元件个数,求ξ的期望.

解:记Ai表示事件:电流能通过Ti,i=1、2、3、4,A表示事件:T1,T2,T3中至少有一个能通过电流,B表示事件:电流能在M、N之间通过.
(I) =
=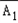
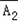
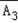 ,(A1,A2,A3相互独立)
,(A1,A2,A3相互独立)
∴P( )=P(
)=P(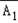
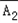
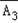 )=P(
)=P(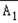 )P(
)P(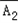 )P(
)P(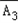 )=(1﹣P)3,
)=(1﹣P)3,
又∵P( )=1﹣P(A)=1﹣0.999=0.001
)=1﹣P(A)=1﹣0.999=0.001
∴(1﹣p)3=0.001,
解之得p=0.9
(II)∵B=A4+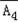 A1A3+
A1A3+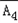
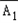 A2A3,
A2A3,
∴P(B)=P(A4)+P(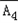 A1A3)+P(
A1A3)+P(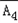
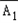 A2A3)
A2A3)
=P(A4)+P(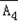 )P(A1)P(A3)+P(
)P(A1)P(A3)+P(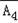 )P(
)P(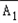 )P(A2)P(A3)
)P(A2)P(A3)
=0.9+0.1×0.9×0.9+0.1×0.1×0.9×0.9=0.9891
即电流能在M与N之间通过的概率为0.991
(III)由于电流能通过各元件的概率都是0.9,且电流能通过各元件相互独立,
用ξ表示T1,T2,T3,T4中能通过电流的元件个数,则ξ服从二项分布,n=4且p=0.9
即ξ~B(4,0.9),
由二项分布的数学期望公式,
得Eξ=4×0.9=3.6
即ξ的期望为3.6
(I)
 =
=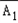
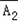
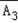 ,(A1,A2,A3相互独立)
,(A1,A2,A3相互独立)∴P(
 )=P(
)=P(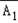
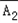
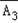 )=P(
)=P(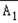 )P(
)P(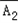 )P(
)P(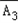 )=(1﹣P)3,
)=(1﹣P)3,又∵P(
 )=1﹣P(A)=1﹣0.999=0.001
)=1﹣P(A)=1﹣0.999=0.001∴(1﹣p)3=0.001,
解之得p=0.9
(II)∵B=A4+
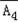 A1A3+
A1A3+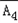
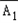 A2A3,
A2A3,∴P(B)=P(A4)+P(
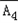 A1A3)+P(
A1A3)+P(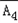
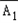 A2A3)
A2A3)=P(A4)+P(
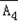 )P(A1)P(A3)+P(
)P(A1)P(A3)+P(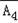 )P(
)P(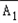 )P(A2)P(A3)
)P(A2)P(A3)=0.9+0.1×0.9×0.9+0.1×0.1×0.9×0.9=0.9891
即电流能在M与N之间通过的概率为0.991
(III)由于电流能通过各元件的概率都是0.9,且电流能通过各元件相互独立,
用ξ表示T1,T2,T3,T4中能通过电流的元件个数,则ξ服从二项分布,n=4且p=0.9
即ξ~B(4,0.9),
由二项分布的数学期望公式,
得Eξ=4×0.9=3.6
即ξ的期望为3.6

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案
相关题目
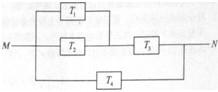 如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是P,电流能通过T4的概率是0.9,电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,T3的概率都是P,电流能通过T4的概率是0.9,电流能否通过各元件相互独立.已知T1,T2,T3中至少有一个能通过电流的概率为0.999.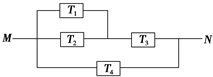 如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,
如图,由M到N的电路中有4个元件,分别标为T1,T2,T3,T4,电流能通过T1,T2,

