题目内容
已知函数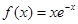 (x∈R).
(x∈R).
(1)求函数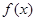 的单调区间和极值;
的单调区间和极值;
(2)已知函数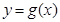 的图象与函数
的图象与函数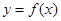 的图象关于直线x=1对称,证明当x>1时,
的图象关于直线x=1对称,证明当x>1时,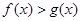 .
.
【答案】
(1) f(x)在(-∞,1)上是增函数,在(1,+∞)上是减函数.故函数f(x)在x=1处取得极大值f(1),且f(1)= (2)见解析
(2)见解析
【解析】本试题主要是考查了导数在研究函数中的运用。
(1)根据已知函数求解导数,结合导数的 符号与单调性的关系得到单调区间。
(2)构造函数由题意可知g(x)=f(2-x),
得g(x)=(2-x)ex-2.
令F(x)=f(x)-g(x),即F(x)=xe-x+(x-2)ex-2.
于是F′(x)=(x-1)(e2x-2-1)e-x.
当x>1时,2x-2>0,从而e2x-2-1>0.
又e-x>0,
结合单调性得到结论。
解:(1)f′(x)=(1-x)e-x.令f′(x)=0,
解得x=1.
当x变化时,f′(x),f(x)的变化情况如下表:
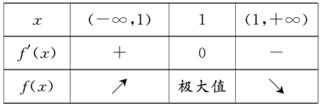
所以f(x)在(-∞,1)上是增函数,在(1,+∞)上是减函数.
故函数f(x)在x=1处取得极大值f(1),且f(1)= .
.
(2)证明:由题意可知g(x)=f(2-x),
得g(x)=(2-x)ex-2.
令F(x)=f(x)-g(x),即F(x)=xe-x+(x-2)ex-2.
于是F′(x)=(x-1)(e2x-2-1)e-x.
当x>1时,2x-2>0,从而e2x-2-1>0.
又e-x>0,
所以F′(x)>0,从而函数F(x)在[1,+∞)上是增函数.
又F(1)=e-1-e-1=0,
所以x>1时,有F(x)>F(1)=0,
因此,当x>1时,f(x)>g(x).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
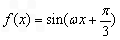 (x∈R,
(x∈R, )的图象如图,P是图象的最高点,Q是图象的最低点.且
)的图象如图,P是图象的最高点,Q是图象的最低点.且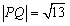 .
.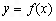 的解析式;
的解析式;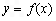 图象向右平移1个单位后得到函数
图象向右平移1个单位后得到函数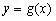 的图象,当
的图象,当 时,求函数
时,求函数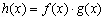 的最大值.
的最大值.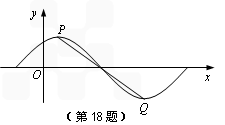
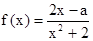 (x∈R)在区间[-1,1]上是增函数.
(x∈R)在区间[-1,1]上是增函数.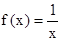 的两实数根为x1、x2,试问:是否存在实数m,使得不等式
的两实数根为x1、x2,试问:是否存在实数m,使得不等式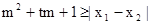 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由? 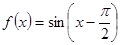 (x∈R),下面结论错误的是 ( )
(x∈R),下面结论错误的是 ( )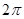 ; B.函数f(x)在区间
; B.函数f(x)在区间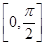 是增函数;
是增函数;