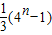题目内容

数列{an}，已知对任意正整数n，a1+a2+a3+…+an=2n-1，则a12+a22+a32+…+an2 等于（　　）
A．（2n-1）2B．
1
3
(2n-1)		C．
1
3
(4n-1)		D．4n-1
∵a1+a2+a3+…+an=2n-1…①
∴a1+a2+a3+…+an-1=2n-1-1…②，
①-②得an=2n-1，
∴an2=22n-2，
∴数列{an2}是以1为首项，4为公比的等比数列，
∴a12+a22+a32+…+an2=
1-4n
1-4
=
1
3
(4n-1)，
故选C．
练习册系列答案
相关题目
数列{an}，已知对任意正整数n，a1+a2+a3+…+an=2n-1，则a12+a22+a32+…+an2 等于（　　）
A、（2n-1）2
B、
1
3
(2n-1)
C、
1
3
(4n-1)
D、4n-1

数列{an}中,已知对任意n∈N*,a1+a2+a3+…+an=3n-1,则+++…+等于(　　)

(A)(3n-1)2 (B) (9n-1)

(C)9n-1 (D) (3n-1)

 
数列{an}，已知对任意正整数n，a1+a2+a3+…+an=2n-1，则a12+a22+a32+…+an2 等于（ ）
A．（2n-1）2
B．
C．
D．4n-1
数列{an}，已知对任意正整数n，a1+a2+a3+…+an=2n-1，则a12+a22+a32+…+an2 等于（ ）
A．（2n-1）2
B．
C．
D．4n-1
数列{an}，已知对任意正整数n，a1+a2+a3+…+an=2n-1，则a12+a22+a32+…+an2 等于（ ）
A．（2n-1）2
B．
C．
D．4n-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网