题目内容
设函数f(x)=ln(x+a)+x2 ,
,
(1)若a= ,解关于x不等式
,解关于x不等式 ;
;
(2)证明:关于x的方程2x2+2ax+1=0有两相异解,且f(m)和f(n)分别是函数f(x)的极小值和极大值(m,n为该方程两根,且m>n).
 ,
, (1)若a=
 ,解关于x不等式
,解关于x不等式 ;
;(2)证明:关于x的方程2x2+2ax+1=0有两相异解,且f(m)和f(n)分别是函数f(x)的极小值和极大值(m,n为该方程两根,且m>n).
(1)解:a= 时,求导函数可得
时,求导函数可得
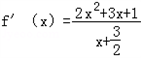 =
=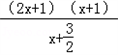 .
.
f(x)的定义域为(﹣ ,+∞).
,+∞).
当﹣ <x<﹣1时,f'(x)>0;
<x<﹣1时,f'(x)>0;
当﹣1<x<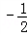 时,f'(x)<0;
时,f'(x)<0;
当x> 时,f'(x)>0.
时,f'(x)>0.
从而,f(x)在(﹣ ,﹣1),(
,﹣1),(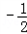 ,+∞)单调增加,在(﹣1,
,+∞)单调增加,在(﹣1,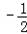 )单调减少.
)单调减少.
∵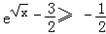 ,f(
,f( )=
)=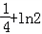
∴不等式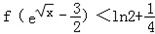 等价于
等价于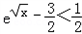
∴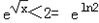
∴0≤x<ln22即所求不等式的解集为{x|0≤x<ln22}.
(2)证明:依题意,f(x)的定义域为(﹣a,+∞),
令g(x)=2x2+2ax+1,因为g(﹣a)=1=g(0)>0,
g(x)的对称轴为x=﹣0.5a>﹣a,△=4a2﹣8a>0(a2>2),g(﹣a)=1>0
∴g(x)在(﹣a,+∞)有两个零点.即方程2x2+2ax+1=0有两相异解
由已知f(x)的定义域为{x|x>﹣a}且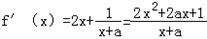 ,
,
若m,n(m>n)方程2x2+2ax+1=0有两相异解,则f'(x)>0的解集为(﹣a,n)∪(m,+∞)(∵a>0)


练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目