题目内容
如图,在三棱锥P﹣ABC中,AB=AC,D为BC的中点,PO⊥平面ABC,垂足O落在线段AD上,已知BC=8,PO=4,AO=3,OD=2
(Ⅰ)证明:AP⊥BC;
(Ⅱ)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.
(Ⅰ)证明:AP⊥BC;
(Ⅱ)在线段AP上是否存在点M,使得二面角A﹣MC﹣β为直二面角?若存在,求出AM的长;若不存在,请说明理由.

解:以O为原点,以AD方向为Y轴正方向,以射线OP的方向为Z轴正方向,建立空间坐标系,则O(0,0,0),A(0,﹣3,0),B(4,2,0),C(﹣4,2,0),P(0,0,4)
(I)则 =(0,3,4),
=(0,3,4), =(﹣8,0,0)
=(﹣8,0,0)
由此可得 ·
·  =0
=0
∴ ⊥
⊥  即AP⊥BC
即AP⊥BC
(II)设 =λ
=λ  ,λ≠1,
,λ≠1,
则 =λ(0,﹣3,﹣4)
=λ(0,﹣3,﹣4) =
= +
+  =
= +λ
+λ  =(﹣4,﹣2,4)+λ(0,﹣3,﹣4)
=(﹣4,﹣2,4)+λ(0,﹣3,﹣4) =(﹣4,5,0),
=(﹣4,5,0), =(﹣8,0,0)
=(﹣8,0,0)
设平面BMC的法向量 =(a,b,c)
=(a,b,c)
则

令b=1,则 =(0,1,
=(0,1, )
)
平面APC的法向量 =(x,y,z)则
=(x,y,z)则 即
即 
令x=5 则 =(5,4,﹣3)
=(5,4,﹣3)
由 =0 得4﹣3
=0 得4﹣3  =0
=0
解得λ= 故AM=3
故AM=3
综上所述,存在点M符合题意,此时AM=3

(I)则
 =(0,3,4),
=(0,3,4), =(﹣8,0,0)
=(﹣8,0,0)由此可得
 ·
·  =0
=0 ∴
 ⊥
⊥  即AP⊥BC
即AP⊥BC (II)设
 =λ
=λ  ,λ≠1,
,λ≠1,则
 =λ(0,﹣3,﹣4)
=λ(0,﹣3,﹣4) =
= +
+  =
= +λ
+λ  =(﹣4,﹣2,4)+λ(0,﹣3,﹣4)
=(﹣4,﹣2,4)+λ(0,﹣3,﹣4) =(﹣4,5,0),
=(﹣4,5,0), =(﹣8,0,0)
=(﹣8,0,0)设平面BMC的法向量
 =(a,b,c)
=(a,b,c)则


令b=1,则
 =(0,1,
=(0,1, )
)平面APC的法向量
 =(x,y,z)则
=(x,y,z)则 即
即 
令x=5 则
 =(5,4,﹣3)
=(5,4,﹣3)由
 =0 得4﹣3
=0 得4﹣3  =0
=0 解得λ=
 故AM=3
故AM=3 综上所述,存在点M符合题意,此时AM=3


练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
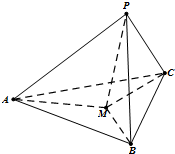 如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=(
如图,在三棱锥P-ABC中,PA、PB、PC两两垂直,且PA=3.PB=2,PC=1.设M是底面ABC内一点,定义f(M)=(m,n,p),其中m、n、p分别是三棱锥M-PAB、三棱锥M-PBC、三棱锥M-PCA的体积.若f(M)=( 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( )
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠ACB=90°,AE⊥PB于E,AF⊥PC于F,若PA=AB=2,∠BPC=θ,则当△AEF的面积最大时,tanθ的值为( ) 如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点.
如图,在三棱锥P-ABC中,PA=PB=AB=2,BC=3,∠ABC=90°,平面PAB⊥平面ABC,D、E分别为AB、AC中点. 如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是
如图,在三棱锥P-ABC中,已知PA=PB=PC,∠BPA=∠BPC=∠CPA=40°,一绳子从A点绕三棱锥侧面一圈回到点A的最短距离是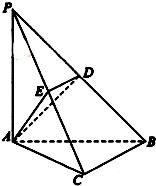 如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱
如图,在三棱锥P-ABC中,PA⊥底面ABC,∠BCA=90°,AP=AC,点D,E分别在棱