题目内容
已知△ABC中,∠A=30°,AB,BC分别是 ,
, 的等差中项与等比中项,则△ABC的面积等于
的等差中项与等比中项,则△ABC的面积等于
- A.

- B.

- C.
 或
或
- D.
 或
或
C
分析:由题意,根据等差数列及等边数列的性质分别求出AB与BC的值,再由A的度数,求出sinA的值,利用正弦定理求出sinC的值,由C为三角形的内角,利用特殊角的三角函数值求出C的度数,根据A和C的度数,利用内角和定理求出B的度数,根据B的度数判断出三角形的形状为直角三角形或等腰三角形,分别求出三角形的面积即可.
解答:∵AB,BC分别是 ,
, 的等差中项与等比中项,
的等差中项与等比中项,
∴AB= ,BC=1,又A=30°,
,BC=1,又A=30°,
根据正弦定理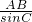 =
=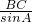 得:sinC=
得:sinC= ,
,
∵C为三角形的内角,∴C=60°或120°,
当C=60°时,由A=30°,得到B=90°,即三角形为直角三角形,

则△ABC的面积为 ×
× ×1=
×1= ;
;
当C=120°时,由A=30°,得到B=30°,即三角形为等腰三角形,

过C作出AB边上的高CD,交AB于点D,
在Rt△ACD中,AC=BC=1,A=30°,∴CD= ,
,
则△ABC的面积为 ×
× ×
× =
= ,
,
综上,△ABC的面积为 或
或 .
.
故选C
点评:此题考查了等差数列、等比数列的性质,正弦定理以及特殊角的三角函数值,利用数形结合及分类讨论的思想,由C的度数有两解,得到三角形的形状有两种,故求出的三角形面积有两解,不要漏解.
分析:由题意,根据等差数列及等边数列的性质分别求出AB与BC的值,再由A的度数,求出sinA的值,利用正弦定理求出sinC的值,由C为三角形的内角,利用特殊角的三角函数值求出C的度数,根据A和C的度数,利用内角和定理求出B的度数,根据B的度数判断出三角形的形状为直角三角形或等腰三角形,分别求出三角形的面积即可.
解答:∵AB,BC分别是
 ,
, 的等差中项与等比中项,
的等差中项与等比中项,∴AB=
 ,BC=1,又A=30°,
,BC=1,又A=30°,根据正弦定理
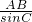 =
=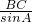 得:sinC=
得:sinC= ,
,∵C为三角形的内角,∴C=60°或120°,
当C=60°时,由A=30°,得到B=90°,即三角形为直角三角形,

则△ABC的面积为
 ×
× ×1=
×1= ;
;当C=120°时,由A=30°,得到B=30°,即三角形为等腰三角形,

过C作出AB边上的高CD,交AB于点D,
在Rt△ACD中,AC=BC=1,A=30°,∴CD=
 ,
,则△ABC的面积为
 ×
× ×
× =
= ,
,综上,△ABC的面积为
 或
或 .
.故选C
点评:此题考查了等差数列、等比数列的性质,正弦定理以及特殊角的三角函数值,利用数形结合及分类讨论的思想,由C的度数有两解,得到三角形的形状有两种,故求出的三角形面积有两解,不要漏解.

练习册系列答案
相关题目