题目内容
设函数f(x)=|2x+1|-|x-4|.(1)解不等式f(x)＞2;
(2)求函数y=f(x)的最小值.
解：(1)令y=|2x+1|-|x-4|,则y=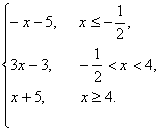
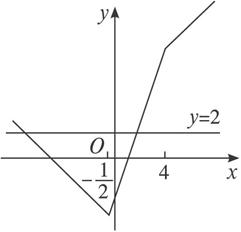
作出函数y=|2x+1|-|x-4|的图象,它与直线y=2的交点为(-7,2)和(
,2).
所以|2x+1|-|x-4|＞2的解集为(-∞,-7)∪(
,+∞).
(2)由函数y=|2x+1|-|x-4|的图象可知,当x=
时,y=|2x+1|-|x-4|取得最小值
.
练习册系列答案
相关题目
设函数f(x)=2
，对于给定的正数K，定义函数fK(x)=
若对于函数f(x)=2
定义域内的任意 x，恒有fK（x）=f（x），则（ ）
| -x2+x+2 |
|
| -x2+x+2 |
A、K的最大值为2
| ||
B、K的最小值为2
| ||
| C、K的最大值为1 | ||
| D、K的最小值为1 |