题目内容
下列命题是真命题的是( )
分析:含有量词的命题的否定,要改量词并且否定后面的结论,故A为真命题;根据充要条件的定义,B中的两个条件是既不充分也不必要条件,故B为假命题;根据向量数量积的定义,可得C是假命题;根据原命题与否命题的关系,得D是假命题.
解答:解:对于A,命题“?x>0,使得x2-2x+3≥0”是含有量词“任意”的命题,
因此将其否定,只需改量词为“存在”并且否定结论即可.
故原命题的否定为“?x>0,使得x2-2x+3<0”,得A为真命题.
对于B,条件p:“0<ab<1”不能推出条件q:“b<
”,
故p不是q充分条件,也不是充分不必要条件,故B不正确.
对于C,向量
,
满足
•
=0,可能
是
互相垂直的非零向量,
不一定有“
=0或
=0”成立,故C是假命题;
对于D,命题“若p,则q”的否命题是“若非p,则非q”
由此可得“若a+b+c=3,则a2+b2+c2≥3”的否命题为“若a+b+c≠3,则a2+b2+c2<3”,故D为假命题.
故选:A
因此将其否定,只需改量词为“存在”并且否定结论即可.
故原命题的否定为“?x>0,使得x2-2x+3<0”,得A为真命题.
对于B,条件p:“0<ab<1”不能推出条件q:“b<
| 1 |
| a |
故p不是q充分条件,也不是充分不必要条件,故B不正确.
对于C,向量
| a |
| b |
| a |
| b |
| a |
| b |
不一定有“
| a |
| b |
对于D,命题“若p,则q”的否命题是“若非p,则非q”
由此可得“若a+b+c=3,则a2+b2+c2≥3”的否命题为“若a+b+c≠3,则a2+b2+c2<3”,故D为假命题.
故选:A
点评:本题以命题真假的判断为载体,考查了向量数量积的运算性质、不等式等价变形和四种命题等知识点,属于基础题.

练习册系列答案
相关题目
 ,对
,对 都有
都有 ,则
,则 为偶函数
为偶函数 ,若对
,若对 ,都有
,都有 ,则函数
,则函数 中心对称
中心对称 与
与 是奇函数
是奇函数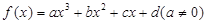 的图形一定是对称中心在图像上的中心对称图形。
的图形一定是对称中心在图像上的中心对称图形。 有两不同极值点
有两不同极值点 ,若
,若 ,且
,且 ,则关于的方程
,则关于的方程 的不同实根个数必有三个.
的不同实根个数必有三个.