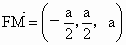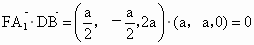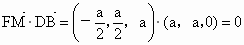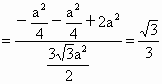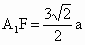题目内容
(2007
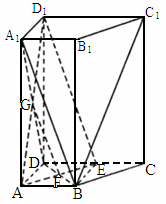
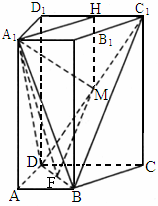
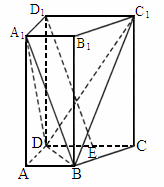
山东,19)如下图,在直四棱柱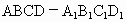 中,已知
中,已知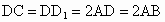 ,AD⊥DC,AB∥DC.
,AD⊥DC,AB∥DC.
(1)
设E是DC的中点,求证: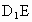 ∥平面
∥平面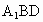 ;
;
(2)
求二面角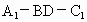 的余弦值.
的余弦值.
答案:略
解析:
解析:
|
解析:解法一: (1)连接BE,则四边形DABE为正方形,
∴ 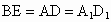 ,且 ,且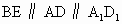 , ,
∴四边形 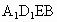 为平行四边形. 为平行四边形.
∴ 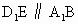 . .
又 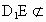 平面 平面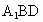 , ,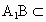 平面 平面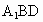 , ,
∴  . .
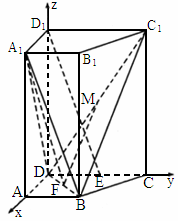
(2) 以D为原点,DA,DC,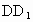 所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,不妨设DA=1,则D(0,0,0),A(1,0,0),B(1,1,0), 所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,不妨设DA=1,则D(0,0,0),A(1,0,0),B(1,1,0),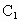 (0,2,2), (0,2,2),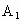 (1,0,2), (1,0,2),
∴ 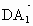 =(1,0,2), =(1,0,2),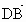 =(1,1,0). =(1,1,0).
设 n=(x,y,z)为平面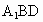 的一个法向量, 的一个法向量,
由 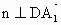 , ,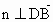 , ,
得 
取 z=1,则n=(-2,2,1).又 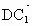 =(0,2,2), =(0,2,2),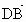 =(1,1,0), =(1,1,0),
设 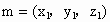 为平面 为平面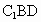 的一个法向量,由 的一个法向量,由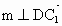 , ,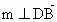 , ,
得 
取 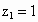 ,则m=(1,-1,1). ,则m=(1,-1,1).
设 m与n的夹角为α,二面角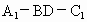 为θ,显然θ为锐角, 为θ,显然θ为锐角,
∴ 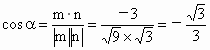 .∴ .∴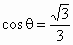 . .
即所求二面角 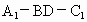 的余弦值为 的余弦值为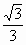 . .
解法二: (1)以D为原点,DA,DC,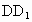 所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系, 所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,
设 DA=a,由题意知:D(0 ,0,0),A(a,0,0),B(a,a,0),C(0,2a,0),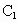 (0,2a,2a), (0,2a,2a),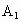 (a,0,2a), (a,0,2a), (0,0,2a),E(0,a,0), (0,0,2a),E(0,a,0),
∴ 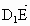 =(0,a,-2a), =(0,a,-2a),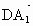 =(a,0,2a), =(a,0,2a),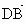 =(a,a,0). =(a,a,0).
又 (0,a,-2a)=(a,a,0)-(a,0,2a),∴ 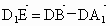 . .
∵ 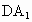 ,DB ,DB 平面 平面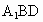 , ,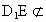 平面 平面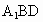 , ,
∴  . .
(2) 取DB的中点F,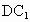 的中点M,连接 的中点M,连接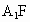 ,FM,由(1)及题意得知 ,FM,由(1)及题意得知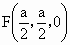 ,M(0,a,a), ,M(0,a,a),
∴ 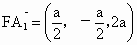 , ,
∴ 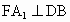 ,FM⊥DB. ,FM⊥DB.
∴ 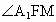 为所求二面角的平面角. 为所求二面角的平面角.
∴ 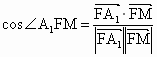
所以二面角 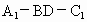 的余弦值为 的余弦值为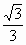 . .
解法三: (1)证明:如解法一图,连接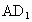 ,AE, ,AE,
设 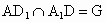 ,AE∩BD=F,连接GF, ,AE∩BD=F,连接GF,
由题意知 G是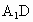 的中点,又E是CD的中点, 的中点,又E是CD的中点,
∴四边形 ABED是平行四边形,故F是AE的中点,∴在 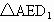 中, 中,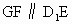 , ,
又 GF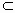 平面 平面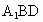 , ,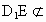 平面 平面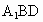 , ,
∴ 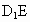 ∥平面 ∥平面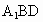 . .
(2) 如图,在四边形ABCD中,设AD=a,
∵ AB=AD,AD⊥DC,AB∥DC,∴ AD⊥AB.故  ,由(1)得 ,由(1)得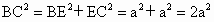 ,DC=2a, ,DC=2a,
∴∠ DBC=90°,即 BD⊥BC.又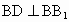 , ,
∴ BD⊥平面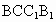 ,又 ,又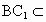 平面 平面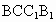 ,∴ ,∴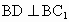 . .
取 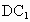 的中点M,连接 的中点M,连接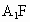 ,FM,由题意知 ,FM,由题意知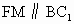 , ,
∴ FM⊥BD.又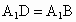 ,∴ ,∴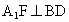 . .
∴ 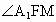 为二面角 为二面角 的平面角, 的平面角,
连接 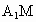 ,在 ,在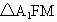 中,由题意知: 中,由题意知:
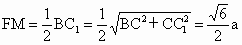 , ,
取 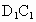 的中点H,连接 的中点H,连接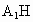 ,HM, ,HM,
在 Rt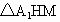 中,∵ 中,∵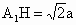 ,HM=a, ,HM=a,
∴ 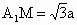 . .
∴ 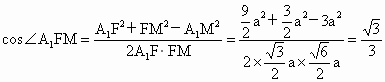 . .
∴二面角 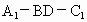 的余弦值为 的余弦值为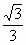 . . |

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目