题目内容
(文科)设一组数据的方差s2,将这组数据的每个数据乘以10,所得到一组新数据的方差是( )
分析:先设原数据的平均数,然后求出每个数据都乘以10后的平均数,最后利用方差公式进行求解即可.
解答:解:设该组数据为x1、x2、x3…xn,则设其平均数为
;若将每个数据都乘以10,则有10x1、10x2、10x3…10xn,则其平均数为10
.
于是原数据方差为:s2=
[(x1-
)2+(x2-
)2+…+(xn-
)2,
新数据方差为:s2=
[(10x1-10
)2+(10x2-10
)2+…+(10xn-10
)2]=100s2.
故选B.
. |
| x |
. |
| x |
于是原数据方差为:s2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
新数据方差为:s2=
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |
故选B.
点评:本题说明了当数据都乘以一个数a时,方差变为原方差a2倍,同时考查了运算能力,属于基础题.

练习册系列答案
相关题目
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 5 | 4 | 3 | 2 |
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
|
组别 |
理科 |
文科 |
||
|
性别 |
男生 |
女生 |
男生 |
女生 |
|
人数 |
4 |
4 |
3 |
1 |
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.(Ⅰ)求理科组恰好记4分的概率?(4分)
(Ⅱ)设文科男生被选出的人数为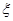 ,求随机变量
,求随机变量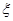 的分布列和数学期望
的分布列和数学期望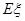 .(8分)
.(8分)
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 5 | 4 | 3 | 2 |
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
某校的学生记者团由理科组和文科组构成,具体数据如下表所示:
学校准备从中选出4人到社区举行的大型公益活动进行采访,每选出一名男生,给其所在小组记1分,每选出一名女生则给其所在小组记2分,若要求被选出的4人中理科组、文科组的学生都有.
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.
| 组别 | 理科 | 文科 | ||
| 性别 | 男生 | 女生 | 男生 | 女生 |
| 人数 | 5 | 4 | 3 | 2 |
(1)求理科组恰好记4分的概率?
(2)设文科男生被选出的人数为ξ,求随机变量ξ的分布列和数学期望Eξ.