题目内容
已知函数f(x)的定义域是(0,+∞),当x>1时,f(x)>0,且f(x•y)=f(x)+f(y),
(1)证明:f(x)在定义域上是增函数;
(2)若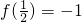 ,解不等式
,解不等式 .
.
证:(1)设x1,x2∈(0,+∞)且x1<x2,则
∴

∴f(x1)<f(x2)∴f(x)在(0,+∞)上是增函数 (5分)
(2)解:令 ,y=1得,
,y=1得,
令x=2,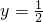 得,
得,
令x=y=2得,f(4)=f(2)+f(2)=2
∴ ,
,
因此, ,即原不等式的解集为[1+
,即原不等式的解集为[1+ ,+∞)(12分)
,+∞)(12分)
分析:(1)要掌握定义法证明单调性的前提是x1<x2,判断f(x2)>f(x1)即可,准确构造条件当x>1时,f(x)>0,取x1,x2∈(0,+∞),且x1<x2, ,进而得出结论;
,进而得出结论;
(2)要利用第一问的结论,加上条件f(x•y)=f(x)+f(y),利用单调性即可解出答案.
点评:本题要掌握定义法证明单调性的前提是x1<x2,判断f(x2),f(x1)的大小;另外如果第一问无法准确得出,可以直接将结论应用于第二问.

∴


∴f(x1)<f(x2)∴f(x)在(0,+∞)上是增函数 (5分)
(2)解:令
 ,y=1得,
,y=1得,
令x=2,
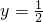 得,
得,
令x=y=2得,f(4)=f(2)+f(2)=2
∴
 ,
,
因此,
 ,即原不等式的解集为[1+
,即原不等式的解集为[1+ ,+∞)(12分)
,+∞)(12分)分析:(1)要掌握定义法证明单调性的前提是x1<x2,判断f(x2)>f(x1)即可,准确构造条件当x>1时,f(x)>0,取x1,x2∈(0,+∞),且x1<x2,
 ,进而得出结论;
,进而得出结论;(2)要利用第一问的结论,加上条件f(x•y)=f(x)+f(y),利用单调性即可解出答案.
点评:本题要掌握定义法证明单调性的前提是x1<x2,判断f(x2),f(x1)的大小;另外如果第一问无法准确得出,可以直接将结论应用于第二问.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
